- The heuristic evaluation function is inaccurate.
- This always happens.
- This cannot happen.
- We are in an infinite loop.
- We are going the wrong way.
- The goal has been wrongly defined.
- t < w ≤ 0
- 0 < w ≤ t
- 0 ≤ t < w
- t ≤ w < 0
- w < t ≤ 0
- w ≤ t < 0
- 0 < t ≤ w
- 0 ≤ w < t
- 2(n-1)
- (n-1)!
- n!
- 2n
- n2
- nn
Temperature 22 degrees, pressure 1000 mb. Rain.
Temperature 15 degrees, pressure 990 mb. No rain.
Then the question is:
Temperature 17 degrees, pressure 1010 mb. Will there be rain?
We predict by Hamming distance to the nearest exemplar, (a) with pressure in millibars, (b) with pressure in bars. What does it predict?
- (a) No rain, (b) No rain
- (a) Rain, (b) No rain
- (a) Rain, (b) Rain
- (a) No rain, (b) Rain
- Generate a graph of the child states of all states.
- Generate a graph of the child states of a tiny percentage of the states.
- Generate a graph of the child states of most of the states.
- Generate a list of the child states of a tiny percentage of the states.
- Generate a list of the child states of all states.
- Generate a list of the child states of most of the states.
- It is never irrelevant.
- wij = 0 for all i and j.
- It is always irrelevant.
- wij = 0 for all j.
- wij = 0 for no j.
- wij = 0 for at least one j.
- It cannot learn to ignore input Ii.
- Moving wii towards 1.
- Moving wjj towards 1.
- Moving wjj towards 0.
- Moving wii towards 0.
- Moving wij towards 0.
- Moving wij towards 1.
f has its (a) highest slope value, and (b) steepest slope (highest absolute value) at:
- (a) y = 1/2, (b) y = 0 or 1
- (a) y = 0 or 1, (b) y = 1/2
- (a) y = 1/2, (b) y = 1/2
- (a) y = 0 or 1, (b) y = 0 or 1
- 100
- 110
- 10
- 10100
- 10010
- 1010
- 1000
- Given a network architecture, an Input leads to an Output after a fixed number of calculations.
- It can be used to represent a function from real-valued multi-dimensional input to real-valued multi-dimensional output.
- Input is compared to previous Input, and "nearby" Input should produce "nearby" Output.
- It can be used to represent a function from real-valued single-dimensional input to real-valued single-dimensional output.
- It can be used to represent any normal linear, continuous, non-chaotic function.
- It can be used to represent any normal non-linear, continuous, non-chaotic function.
- It can be used to represent a function from integer-valued multi-dimensional input to integer-valued multi-dimensional output.
- As learning progresses, the size of the network remains fixed.
- Divide by zero error.
- It would take too long.
- Learning it from exemplars is impossible for some values of x.
- Learning it from exemplars is impossible.
- It is a chaotic function.
- There is nothing to learn. The problem is solved.
- We would learn it from exemplars.
- Best-first search will eliminate all bias.
- Nodes on the left are not searched first.
- Yes. But a heuristic can be used to eliminate all bias.
- Yes. But it is rarely a problem.
- No.
- Yes. But a heuristic can be used to produce a bias that is better than random.
- Yes. But it is alright because all nodes will be searched eventually.
- Yes. But it is never a problem.
- Domain-specific heuristic, Random search, Metaheuristic
- Domain-specific heuristic, Metaheuristic, Random search
- Random search, Metaheuristic, Domain-specific heuristic
- Metaheuristic, Random search, Domain-specific heuristic
- Random search, Domain-specific heuristic, Metaheuristic
- Metaheuristic, Domain-specific heuristic, Random search
x7 = w17 y1 + w27 y2 + w37 y3
Then ∂x7 / ∂w27 is:
- yj
-
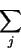 wjk
wjk
-
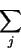 yj
yj
- w27
- y2
- wjk
When input is (x1) output should be (a1).
When input is (x2) output should be (a1).
When input is (x1) output should be (a2).
How can this happen?
- There are missing inputs, or the world is probabilistic.
- The 2nd exemplar can happen but not the 3rd.
- The machine is badly programmed.
- This cannot happen.
- This always happens.
- The 3rd exemplar can happen but not the 2nd.
- 101 n
- 101 + n
- 100 + n
- 101 n + 1
- 102 n
- 100 n
- 102 n + 1
- 100 n + 1
An example showing that this is this a bad measure of the error is: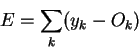
- y = (5,0,5), O = (-5,0,5)
- y = (5,0,-5), O = (-5,0,-5)
- y = (5,0,5), O = (-5,0,-5)
- y = (-5,0,5), O = (-5,0,5)
- y = (5,0,-5), O = (-5,0,5)
- y = (5,0,5), O = (5,0,5)
- n
- x
- xn
- nx
- x + x2 + x3 + ... + xn
- x+xn
- xx
- nx
y = a x + bDefine a perceptron that receives x and y as input and fires if and only if the point is on this side of the line:
y ≤ a x + b
- weights: -a, 1, threshold: -b
- weights: a, -1, threshold: b
- weights: -a, 1, threshold: b
- weights: a, -1, threshold: -b
- Constant output 0.
- Constant output 1.
- XOR
- None of the above.
- OR
- AND
- NOT