State space Search

3.1.3 - State space representation of problem

1. All the states the system can be in are represented as nodes of a graph.
2. An action that can change the system from one state to another (e.g. a move in a game) is represented by a link from one node to another.
3. Links may be unidirectional (e.g. Xs and Os, can't go back) or bi-directional (e.g. geographic move).

4. Search for a solution.
5. A solution might be:
   1. Any path from start state to goal state.
   2. The best (e.g. lowest cost) path from start state to goal state (e.g. Travelling salesman problem).
6. It may be possible to reach the same state through many different paths (obviously true in Xs and Os).
7. There may be loops in the graph (can go round in circle). No loops in Xs and Os.

Xs and Os

• Xs and Os
• Directed acyclic graph
• Unidirectional. No loops. Multiple paths to the same state.
• Multiple goal states.

• Game-tree complexity
  • 9 first moves, 8 replies, 7 replies, ...
  • 9! (9 factorial) = 362,880 different paths.
  • In fact, 9! is an upper bound - many of these games will terminate with a win before reaching end of path.
  • Number of paths < 9!
  • Unlike chess, could do exhaustive search.

• State-space complexity
  • How many unique states exist?
  • Could have blank, X or O in each of 9 squares.
  • That is 3⁹ = 19,683 different states.
  • In fact, this is an upper bound - many of these states don't exist. e.g. 9 X's.
  • These states don't exist:
    1. (Number of Xs) - (Number of Os) = 2 or more
    2. (Number of Os) - (Number of Xs) = 2 or more

  • Q. Is this a complete list of non-existent states?

Reduce statespace

See Luger Fig 4.1

• Symmetry reduction on 1st level reduces no. of paths to 3 . 8!
• Symmetry reduction on 2nd level reduces no. of paths to 12 . 7! = 60,480

Symmetry reduction may require a lot of work by the human. But worth it if it reduces search problem (sometimes massively).
We write code to do the transform, search and transform back.

Travelling salesman problem (TSP)

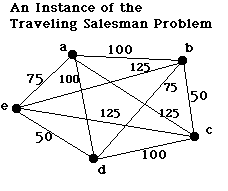
Travelling salesman problem.
Start at A, visit all cities, return to A. Links show cost of each trip (distance, money). Find trip with minimum cost.
Solution is a path. e.g. [A,D,C,B,E,A]
Image courtesy of Ralph Morelli.
See Luger Fig 3.9

Q. What is the shortest path?

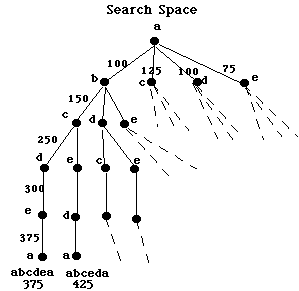
Q. What assumption did we make?

Q. When do we stop the search?

How big is the TSP?

• Given n cities, (n-1) choices for 1st stop, (n-2) choices for next stop, etc.
  Q. What assumption did we make?
• (n-1)! paths
  With many cities or nodes this soon becomes intractable.

Restrict search / Problem-specific heuristics

Reduce statespace

Heuristic search

Luger changes his numbers to show example of "Nearest neighbour" heuristic failing on Travelling salesman problem:

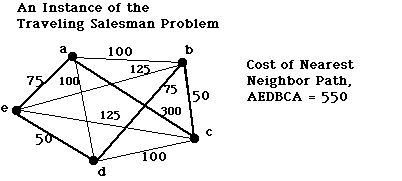
Image courtesy of Ralph Morelli.
See Luger Fig 3.11

3.2 - Searching a statespace graph

3.2.2 - Backtracking (exhaustive search)

Depth-first search

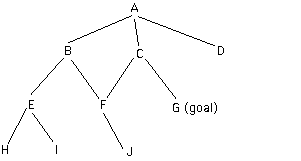
Depth-first search:
Start at A. Search state space systematically until find goal.
When multiple children, go down 1st child. If fails, back to parent, down 2nd child, and so on.
Image courtesy of Ralph Morelli.
See Luger Fig 3.14

Note there are multiple paths to F.
If F has already been found to be a dead-end when we went there from B, the algorithm should not go there a second time (from C).
However not a great example here since C can see goal so won't go to F anyway.

function newchildren ( state )
{
  returns not all the children of state,
  but the new ones to look at
  i.e. those not on DE, SL or NSL
}

SL := [Start]			// CS is part of the chain
NSL := [Start]
DE := []
CS := Start  

while NSL not empty do
{
  if CS = goal  
    return SL
                    
  else if newchildren(CS) not empty 
  {
    place newchildren(CS) on NSL
    CS := first element of NSL	// move down to new state
    add CS to SL			// CS is part of the chain
  }

  else 			// newchildren(CS) empty, so backtrack 
  {
    while (SL not empty) and (CS == first element of SL) 
    {
              add CS to DE 
              remove first element of SL                
              remove first element of NSL
              CS := first element of NSL
    }
    add CS to SL
  }
}

Breadth-first search

Depth-first search examines the nodes in the order:

  A, B, E, K, S, L, T, F, M, C, G, N, H, O, P, U, D, I, Q, J, R

Need to:

• Keep track of current path from start. Keeps changing as we search down.
• Keep track of dead ends - have searched all below this state.
• Keep track of known states not yet searched - will be quite small.

  A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U

• Keep track of known states not yet searched - will grow massively, since it is all cousins at the current level down.

  function newchildren ( state )
  {
   return children of state that are not already on OPEN or CLOSED   
  }

  OPEN := [Start] 
  CLOSED := []

  while OPEN not empty
  {
      remove LHS state from OPEN, call it X
      if X is goal
          return success 
      else 
      {
          put X on CLOSED
          put newchildren(X) on RHS of OPEN    
      }
  }