Building a prediction machine using distance

We have established the idea of learning from exemplars.
Let us build our first prediction machine.

No interpolation. No extrapolation. Just memory.

The algorithm will be:

Given a new input x,
find the past exemplar with the smallest distance from x.
Return the output for that past exemplar.

Distance in Multi-dimensions

If x is multi-dimensional - Then what is "nearby"?

Here is one possibility. Let x = (x₁,..,x_n) and y = (y₁,..,y_n). Define the Hamming distance between x and y as:

If x and y are vectors of binary digits, then the Hamming distance is just equal to the number of points at which x and y differ.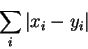

Now, our algorithm could be:

Given a new input x,
find the past exemplar with the smallest Hamming distance from x.
Return the output for that past exemplar.

Hamming distance adds different quantities

The problem with this can be seen in the following.
Let the exemplars be:

Temperature 22 degrees, pressure 1000 millibars. No rain.
Temperature 15 degrees, pressure 990 mb. Rain.

Then the question is:

Temperature 17 degrees, pressure 1010 mb. Will there be rain?

The Hamming distance from the first exemplar is 5 + 10, the distance from the second is 2 + 20. So we say it is nearest to the first exemplar.

However, we have just added together two different quantities - degrees and millibars! We could just as easily have said the exemplars were:

Temperature 22 degrees, pressure 1 bar. No rain.
Temperature 15 degrees, pressure 0.990 bars. Rain.

and the question:

Temperature 17 degrees, pressure 1.010 bars. Will there be rain?

Then the distance is 5 + 0.010 from the first, 2 + 0.020 from the second. The second exemplar is closer.

Which is correct? Which one are we closer to?

The answer is really: If it rains, we must have been closer to the second exemplar. If it doesn't rain, we must be closer to the first. "Closer" is defined by observing the output, rather than pre-defined as in a distance metric.

Same issue with any distance metric

The same applies to any other distance metric, such as the "real" distance metric - the distance between 2 points x = (x₁,..,x_n) and y = (y₁,..,y_n) in n-dimensional Euclidean space:

(e.g. consider n=2 or n=3).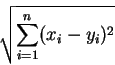

Again, we can change the scale of one axis without the other, and so change the definition of the "nearest" exemplar. It is just easier to show this with the Hamming distance.

Distance metric weighs every dimension the same

Even if we do not have the above problem of heterogenous inputs, a distance metric is still a primitive form of predictor.

e.g. Consider classifying a bitmap of 100 x 100 pixel images.
The components of the input are all the same type of thing - pixels that are, say, 0 (black) or 1 (white).
The distance metric is the number of pixels that are different.
This strategy of looking at distance from exemplars is called template matching.

The basic problem with it is that it weighs every dimension (every pixel) as of equal importance.

Some inputs are more relevant than others

Consider bitmaps of faces. We are trying to distinguish happy faces from sad faces. Say we introduce a new, happy face with a similar haircut to one of the exemplars with a sad face (i.e. we were told: "This face is sad"). The haircut area of the bitmap scores so many hits under the distance metric that this becomes the exemplar that matches, and we guess that the new input is a sad face.

In fact, matching the exemplar with the same haircut / background / ears is a reasonable first guess - after all, how does the machine know in advance that it should be looking at the mouth and eyes, and ignoring the other parts?

The problem is the system cannot learn this. The distance metric is fixed. It cannot learn that some parts of the input space are irrelevant.

Google Reverse Image Search: Sometimes matches the "wrong" part of the image. It does not know what part of the image you are looking for.

Workarounds:

If we get enough exemplars, with happy and sad faces of every haircut, then happy face with some haircut will be closest to a happy exemplar with same haircut, rather than sad exemplar with same haircut, and distance metric will work again.
Also we can try to pre-process the input to only show mouth and eyes. Of course, this assumes we know which are the most important inputs ourselves, which may be true in this simple case but not in many other problems.

Wish list - an algorithm that learns which inputs are important

It would be more useful, and could be applied to much more problems, if the machine could learn which are the most important inputs, and learn to weigh some higher than others because they have a stronger affect on output. We just feed inputs into it. If they are irrelevant it will learn to ignore them.

Performance - Do we have to compare to all other exemplars?

Does our algorithm have to compare current input to all previous exemplars?
This will not scale well. It will take a long time to compare every pixel of the input with every pixel of a large number of previous exemplars (and it must be compared to them all, every time).
And the list of exemplars to compare to keeps getting larger.