Building up a running average

How to build up a running average of samples without needing an ever-growing memory of all samples as you go along.

Let

be samples of a stationary random variable d with expected value E(d). Then the following update algorithm provides an elegant way of sampling them. Repeat:

Proof: D's updates go:

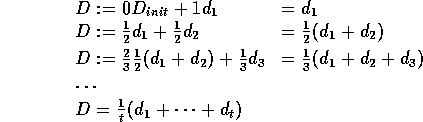
displaymath9187

i.e. D is simply the average of all samples so far.

As , .

Notation: "Adjust in direction of"

I use the notation:

to mean we adjust the estimate D once in the direction of the sample d.

If we store D explicitly as a variable, we may update:

where is the learning rate.
If d < D then the running average D goes down.
If d > D then the running average D goes up.
If D is not stored as a variable, but is the output of a neural network, we may backpropagate the error D - d .

The notation:

means that over many such updates the estimate D converges to the expected value of the samples d.

If d is bounded, then D is bounded

Let D be updated by:

where d is bounded by , , and the initial value of . Then:

Proof: The highest D can be is if it is always updated with :

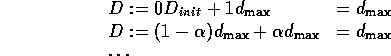
displaymath9303

so . Similarly .

α must start at 1 to get rid of D_init

Thereafter α can be anything from 0 to 1.

Learning rate must be between 0 and 1

Learning rate α is like a probability.
It only makes sense if it is between 0 and 1.

e.g. Imagine if α starts at 1, and thereafter we let α = 11.
Say we get a non-zero sample d once, then 0 forever.
Samples: d, 0, 0, ....
Then D ends up with no apparent relationship to the samples d and 0.
And D is not even bounded. It goes:

D := 0 + 1.d (since α starts at 1)
D := -10 d + 0
D := -10 (-10 d) + 0
D := - 10³ d
D := 10⁴ d
D := - 10⁵ d
....
D not bounded

α not between 0 and 1 makes no sense.

Constant learning rate (time-weighted)

An alternative approach is to build up not the average of all samples, but a time-weighted sum of them, giving more weight to the most recent ones. This is accomplished by setting to be constant, in which case D's updates go:

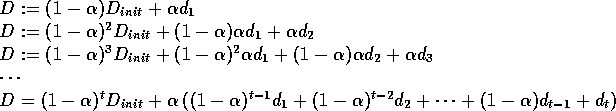
displaymath9240

Since as , this weights more recent samples higher.

Typical learning rate might be .