Building a model of Pxa(r)

---

Build a model as we learn

As Q-learning progresses, the agent experiences the world's transitions. It does not normally build up an explicit map of of the form . Instead it sums the rewards to build up the probably more useful mapping . In fact this exact mapping itself is not stored, but is only one component of the Q-values, which express more than just immediate reward. If the Q-values express the exact map .

But we could build a map of if we wanted.

---

Data structure to represent P_xa(r)

x,a,r -> [0,1]
could be hard map to build.
What if r comes from the world (e.g. stock prices), rather than a finite pre-defined list of r's.
r-space could be huge / hard to define / hard to define limits
Even within limits, what if r is real number.

---

P_xa(r) is too much info

P_xa(r) not very useful. Say in state x and:
P_xa(r=1) = 0.5, P_xa(0) = 0.3, P_xa(-1) = 0.2,
and:
P_xb(3) = 0.5, P_xb(-3) = 0.5.
Take action a or b? How do we decide? Too much info! We want to know E(r) for action decision.
And this is what Q-value is (or, even more useful, E(R)).
Exercise - What is E(r) for each action?

---

E(r) loses information

Maybe P_xa(r) is useful where there is a large standard deviation:
P_xb(100) = 0.5, P_xb(-100) = 0.5.

Q. What is E(r)?

E(r) doesn't tell full story here. May want to avoid the -100 at all costs.

[Although solution here, if you really must avoid a certain punishment, is simply make that punishment -1000 (while keeping positive rewards fixed to less than 100). The machine will soon learn to avoid it.]
In other words, who is to say that -100 is a big punishment? It looks big, but if most rewards are +1000, then it is actually a small punishment. What matters is not the absolute sizes of r's, but their relative sizes.

---

Is -100 a big punishment?

A machine with reward function: "if good thing r = 1 million, if bad thing r = -1 million, else r = 0" will perform no different to a machine with reward function: "if good thing r = 1, if bad thing r = -1, else r = 0"
Proof: See following.

---

Multiply r's by constant, or Add constant to all r's

Q(x,a) =

1. If multiply all rewards by some constant c > 0, then multiply all Q-values by c.
   Same policy (if c > 0).
   If c < 0, it will change the order of Q-values. Also it will change Q-values themselves, since future policy will be changed, since good r's are now bad r's (remember Q(x,a) = reward for a, plus the best you can do thereafter).
   If c=0, random policy.

2. If add some constant c to all rewards, then add:

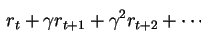
   c + γ c + γ² c + ..

   to all Q-values.
   Same policy, whether c positive or negative.

Proof follows.

---

2-reward reward functions

Consider an agent of the form:

  
 	reward: if (good event) r else s 

where r > s.

Proof: Let us fix r and s and learn the Q-values.

1. In a deterministic world, given a state x, the Q-value for action a will be:

   

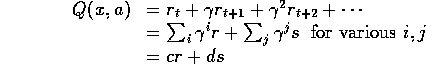
   for some real numbers . The Q-value for a different action b will be:

   

   where . That is, e + f = c + d .

   So whichever one of c and e is bigger defines which is the best action (which gets the larger amount of the "good" reward r), irrespective of the sizes of r > s.

   To be precise, if c > e, then Q(x,a) > Q(x,b)
   Proof: Let c + d = e + f = G
   Q(x,a) = c r + (G-c) s
   Q(x,b) = e r + (G-e) s
   Q(x,a) - Q(x,b) = (c - e) r + (-c + e) s
   = (c - e) (r - s)
   > 0
   Note that these numbers are not integers - it may not be simply a question of the worse action receiving s instead of r a finite number of times. The worse action may also receive r instead of s at some points, and also the number of differences may in fact not be finite.

   To be precise, noting that (c-e) = (f-d) , the difference between the Q-values is:

   

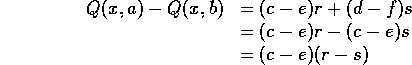
   where the real number (c-e) is constant for the given two actions a and b in state x. (c-e) depends only on the probabilities of events happening, not on the specific values of the rewards r and s that we hand out when they do. Changing the relative sizes of the rewards r > s can only change the magnitude of the difference between the Q-values, but not the sign. The ranking of actions will stay the same.

   For example, an agent with rewards (10,9) and an agent with rewards (10,0) will have different Q-values but will still suggest the same optimal action .

   
   

2. In a probabilistic world, we would have:

   

   where p + q = 1 , and:

   E(rt+1)	= Σ y   Pxa(y)   r(x,y)
   	= Pxa(y1)   r(x,y1) + ... + Pxa(yn)   r(x,yn)
   	= p' r + q' s

   for some p' + q' = 1 .

   Hence:

   

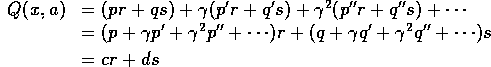
   for some as before.

---

Normalisation

Any 2-reward agent of the form:

  
 	reward: if (good event) r else s 

where r > s, can be normalised to the form:

  
 	reward: if (good event) (r-s) else 0

From Theorem C.1, this will have different Q-values but the same Q-learning policy. You can regard the original agent as an (r-s), 0 agent which also picks up an automatic bonus of s every step no matter what it does. Its Q-values can be obtained by simply adding the following to each of the Q-values of the (r-s), 0 agent:

---

Exaggeration

Say we have a normalised 2-reward agent :

  
 	reward: if (good event) r else 0

where r > 0 .

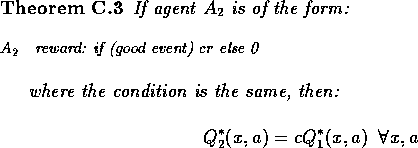
Proof: We have just multiplied all rewards by c, so all Q-values are multiplied by c. If this is not clear, see the general proof Theorem D.1 below.

I should note this only works if: c > 0

will have the same policy as . We are exaggerating or levelling out the contour in this Figure:

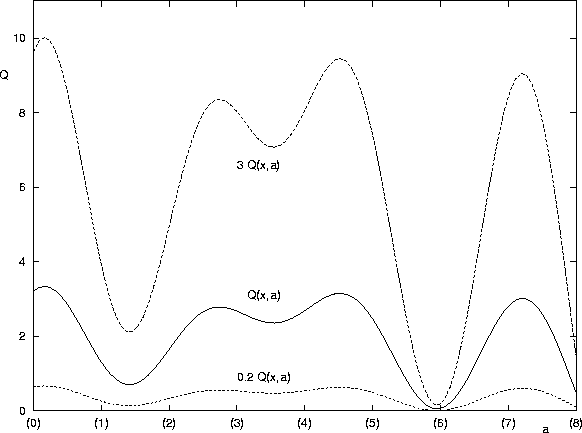
Multiplying the reward by a factor multiplies the Q-values by that factor, which either exaggerates or levels out the contour . The agent will still rank the actions in the same order, and still suggest the same preferred action.

---

Transforming a 2-reward reward function

 if (good event) 10 else 5

is the same as (add -5):

 if (good event) 5 else 0

same as (multiply by 2/5):

 if (good event) 2 else 0

same as (add 3):

 if (good event) 5 else 3

In general:

 if (good event) r1 else r2

is the same as:

 if (good event) (r1-r2) else 0

same as (multiply by something positive, r3 > r4):

 if (good event) (r3-r4) else 0

same as:

 if (good event) r3 else r4

So any 2-reward fn can be transformed into any other, provided we don't change the order of the rewards.

---

3-reward (or more) reward functions

This does not hold with 3-reward (or more) fns.
Any 3-reward fn can not be transformed into any other.

For 3-reward (or more) agents the relative sizes of the rewards do matter for the Q-learning policy. Consider an agent of the form:

  
 	reward: if (best event)    else if (good event)    else    

where .

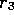
We show by an example that changing one reward in this agent while keeping others fixed can lead to a switch of policy. Imagine that currently actions a and b lead to the following sequences of rewards:

 (x,a) leads to sequence    and then    forever

(x,b) leads to sequence    and then    forever

Currently action b is the best. We lose on the fifth step certainly, but we make up for it by receiving the payoff from in the first four steps. However, if we start to increase the size of , while keeping and the same, we can eventually make action a the most profitable path to follow and cause a switch in policy.

---

Normalisation

Any agent with rewards can be normalised to one with rewards . The original agent can be viewed as a normalised one which also picks up every timestep no matter what.

The normalised agent will have the same policy.

---

Exaggeration

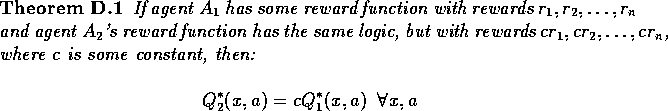
Think of it as changing the "unit of measurement" of the rewards.

Proof: When we take action a in state x, let be the probability that reward is given to (and therefore that reward is given to ). Then 's expected reward is simply c times 's expected reward:

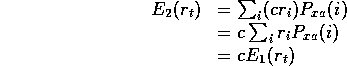
It follows that and .

This only works if: c > 0

will have the same policy as .

---

Transforming a 3-reward reward function

 if (good event) r1 else if (bad event) r2 else r3

where r1 > r3 > r2 (note order),
is the same as:

 if (good) (r1-r3) else if (bad) (r2-r3) else 0

i.e. (where (r3-r2) positive):

 if (good) (r1-r3) else if (bad) - (r3-r2) else 0

same as:

 if (good) (r4-r6) else if (bad) - (r3-r2)(r4-r6)/(r1-r3) else 0

same as:

 if (good) r4 else if (bad) r6 - ((r3-r2)(r4-r6)/(r1-r3))  else r6

Can get 1st and last rewards to anything, but then restricted in what middle reward can be.
Can't transform it into arbitrary r5.

Note that the "bad" reward is indeed less than both r4 and r6:

Note the 3 components here are positive, so:

  (r3-r2)(r4-r6)/(r1-r3) > 0

So:

  r6 - ((r3-r2)(r4-r6)/(r1-r3)) < r6

And:

  r6 < r4

---

Summary of designing reward functions

2-rewards - only 1 good thing - 1 goal - will always pursue it

3-rewards - 2 good things - 2 goals - many ways to balance how you pursue both - a few hits of middle r may compensate for losing one high r - may pursue middle r and ignore higher one

ancientbrain.com      w2mind.org      humphrysfamilytree.com

On the Internet since 1987.      New 250 G VPS server.

Note: Links on this site to user-generated content like Wikipedia are highlighted in red as possibly unreliable. My view is that such links are highly useful but flawed.