Multi-layer Neural Networks

Now we understand the single-layer neural network, let us look at the multi-layer neural network.

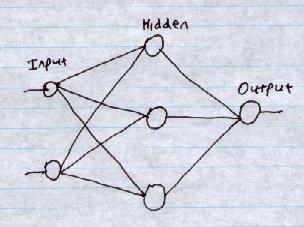
That is, a network with multiple layers of links. This involves what are called "hidden" nodes. This is nothing to do with security. This just means they are not "visible" from the Input or Output sides. Rather they are inside the network somewhere.

Multi-layer Neural Networks allow much more complex classifications.
Consider the network:

The 3 hidden nodes each draw a line and fire if the input point is on one side of the line.

The output node could be a 3-dimensional AND gate - fire if all 3 hidden nodes fire.

3-dimensional AND gate

3 inputs. Let the 3 weights be 1.
Then what threshold to implement an AND gate?
What threshold to implement an OR gate?

In visual terms, the AND gate is separating the point

 (1,1,1)

from the points:

(0,0,0),
(0,1,0),
(0,0,1),
(0,1,1),
(1,0,0),
(1,1,0),
(1,0,1)

Imagine a 3-d cube defined by these points. The 3-dimensional AND gate perceptron implements a 2d plane to separate the corner point (1,1,1) from the other points in the cube.

Exercise

Construct a triangular area from 3 intersecting lines in the 2-dimensional plane.

Define the lines exactly (i.e. express them in terms of y = ax + b).
Define the weights and thresholds of a network that will fire only for points within the triangular area:
1. Define the weights and thresholds for the 3 hidden nodes.
2. Define the weights and threshold for the output node.

Disjoint areas

To only fire when the point is in one of the 2 disjoint areas:

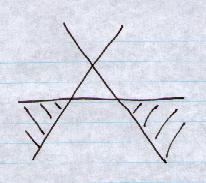
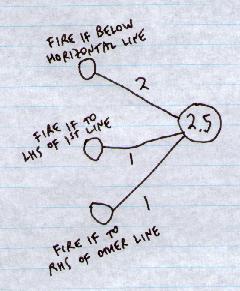
We could have 4 perceptrons, 2 AND gates and a final OR gate.

This hand-designed network will also do the job. (Just Hidden and Output layers shown. Weights shown on connections. Thresholds circled on nodes.):

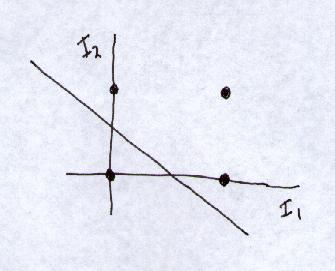
3-layer network can classify any arbitrary shape in n dimensions

A 2-layer network can classify points inside any n arbitrary lines (n hidden units plus an AND function).
i.e. It can classify:

any regular polygon
any convex polygon
any convex set to any level of granularity required (just add more lines)

To classify a concave polygon (e.g. a concave star-shaped polygon), compose it out of adjacent disjoint convex shapes and an OR function. A 3-layer network can do this.

A 3-layer network can classify any number of disjoint convex or concave shapes. Use 2-layer networks to classify each convex region to any level of granularity required (just add more lines, and more disjoint areas), and an OR gate.

Then, like the bed/table/chair network above, we can have a net that fires one output for one complex shape, another output for another arbitrary complex shape.

And we can do this with shapes in n dimensions, not just 2 or 3.

Universal approximation theorem

Reading

Hornik et al - Proves that a multi-layer network can approximate functions.
- "Multilayer feedforward networks are universal approximators". Kurt Hornik, Maxwell Stinchcombe, Halbert White. Neural Networks, Volume 2, Issue 5, 1989, Pages 359-366.
- Proves that multi-layer neural networks can approximate "any Borel measurable function" "to any desired degree of accuracy".

Multi-layer network for XOR

Recall XOR.

We can implement XOR using 2 perceptrons and an AND gate.

This hand-designed network will also do the job:

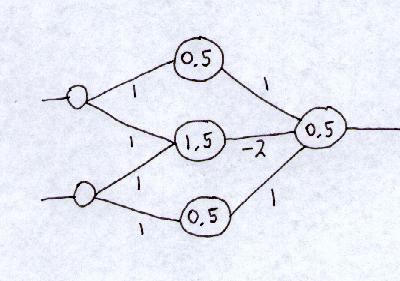
2 connections in first layer not shown (weight = 0).
We have multiple divisions. Basically, we use the 1.5 node to divide (1,1) from the others. We use the 0.5 nodes to split off (0,0) from the others. And then we combine the outputs to split off (1,1) from (1,0) and (0,1).

Stop designing networks

Question - How did we design the XOR network?
Answer - We don't want to. Neural networks wouldn't be popular if you had to.

We want to learn these weights.
We want an algorithm where we can repeatedly present the network with exemplars:

Input 0 0	  Output 0
Input 1 0	  Output 1
Input 0 1	  Output 1
Input 1 1	  Output 0

and it will learn those weights and thresholds.
(Or at least, some set of weights and thresholds that implements XOR.)

Supervised Learning

The idea of Supervised Learning with a neural network is as follows:

Send in an input x.
Run it through the network to generate an output y.
Tell the machine what the "right" answer for x actually is (we have a large number of these known Input-Output exemplars).
Comparing the right answer with y gives an error quantity.
Use this error to modify the weights and thresholds so that next time x is sent in it will produce an answer nearer to the correct one.

The bit in yellow is the hard part.

Interference - both problem and solution

The trick in adjusting weights and thresholds is that at the same time as adjusting the network to make it give a better answer for the current input, we are trying to adjust the weights and thresholds to make it give better answers for other inputs. These adjustments may interfere with each other.
But of course, interference is what we want!
If different inputs didn't interfere with each other, it wouldn't be a generalisation (able to make predictions for inputs never seen before). It would be a lookup table (unable to give an answer for inputs never seen before).
So interference is both problem and solution - a worry for us when we adjust weights, and the solution to having a prediction machine for unseen inputs.