Machine Learning - Introduction

Let us consider the idea of machine "learning".
In machine evolution, a program is fixed and we see what its fitness is, and we make new ones.
In machine learning, a program improves over time, over repeated learning interactions of some sort.

But what exactly does "learning" mean?

What is Learning?

It must be more than just memory:

Human:		The capital of Ireland is Dublin.
Machine:	OK.
Human:		The capital of France is Paris.
Machine:	OK.
Human: 		What is the capital of Ireland?
Machine:	Dublin.
Human:		Brilliant.

The machine should learn something new.

Generalisation - Learning a function from exemplars

Here is one way of expressing the idea of learning something new.

We have experience of a finite number of situations. We must generalise our experience to a new situation, where we have never been told the answer, and make a good guess, where we are not simply recovering a past answer from memory.

Human:		In situation x1, answer is a1.
Human:		In situation x2, answer is a2.
Human:		In situation x3, answer is a3.
Human:		In situation x4, what is answer?
Machine:	f(x4).

where the machine is "learning" the function f.

Each Input-Output pair (xi, ai) that we show to the machine is called an exemplar.
Learning from exemplars like this is called supervised learning.

What would learning from exemplars look like?

f(x4) might be an interpolation (if x4 is between 2 of the points x1,..,x3).
Or f(x4) might be an extrapolation (if x4 is outside the previous points).
For example, the machine might progress as follows:

Human:		In situation x1, answer is a1.
Machine:	OK. I am building a function f(x). 
		Currently, f(x) = a1 for all x.

Human:		In situation x2, answer is a2.
Machine:	f is becoming a more complex mapping, 
		that gives different results for different x.
		e.g. Perhaps currently f((x1+x2)/2) = (a1+a2)/2.

If we have 2 points so far, we may (so far) assume f is a straight line.
Q. What is the equation of f(x)?


Human:		In situation x3, answer is a3.
Machine:	f is getting more complex.

Maybe now f is no longer a straight line.

Human:		In situation x4, what is answer?
Machine:	Using my current definition of f, my answer is f(x4).

Imagine how this line changes

Imagine how this line changes with new data.

If x=0, answer is 0.
If x=100, answer is 100.
If x=50, answer is 95.

If x=25, what is answer?

Regression

Constructing a line or more complex function to fit data is an old problem in statistics.

Regression analysis. The general field of predicting or calculating a function to relate input to output from a limited set of exemplars.
Input - x - independent variable / explanatory variable
Output - y - dependent variable
Linear regression. Special case that constructs the function as:
- A straight line (for single-dimensional input) (simple linear regression)
- Or a hyperplane (for multi-dimensional input) (multiple linear regression)

Equation or data structure?

One approach (statistics, mathematics) is to try to find an equation for the function.

e.g. Least squares method in linear regression minimizes the sum of the squares of the errors (difference between exemplar output and output according to the function). Can follow a calculation to get an equation for the function.

Another approach (computer science) is to build a machine (algorithm plus data structure) to represent the function.

Build a machine that generates outputs for inputs.
Modify the machine to reduce error in prediction.
Normally have a standard algorithm to produce answers given a data structure. Then modify the data structure.
e.g. Data structure is 10,000 parameters. Each particular set of parameters defines one particular function from input to output. There are a large number of possible sets of parameters, so this approach can represent a large number of functions.
May not have any easy to read equation at the end.
More complex machine (larger data structure) needed to represent more complex function.

What type of function - Chaotic functions

The idea of representing a function from exemplars would be that "nearby" Input should generate "nearby" Output.

But some functions defeat this idea. We can quite easily construct functions where nearby input does not lead to nearby output. These are called chaotic functions. These functions may defeat learning from exemplars.

What type of function - Non-linear, Non-chaotic functions

We do not expect that the learning method from exemplars will be able to learn to represent a chaotic function (or a function in a region where it is behaving chaotically).
To represent the chaotic area the function would have to be learnt to an impractically (perhaps infinitely) high level of granularity.

However we do hope that our unknown function is not actually perverse enough to be chaotic, at least in some local regions.

For instance, if you view our Chaos Theory demo function as a function in λ as well as x, then there are regions of that multi-dimensional space in which it is not chaotic.
y = f(x,λ)
x and λ are 2 dimensions
y is the 3rd dimension

We imagine that non-linear but non-chaotic functions can be approximated to acceptable accuracy by a limited size data structure.
In general, the smaller the data structure, the more crude the representation of the function.

Example non-linear function

We expect that the learning method can cope with any reasonably well behaved non-linear, continuous function. For instance, the function:

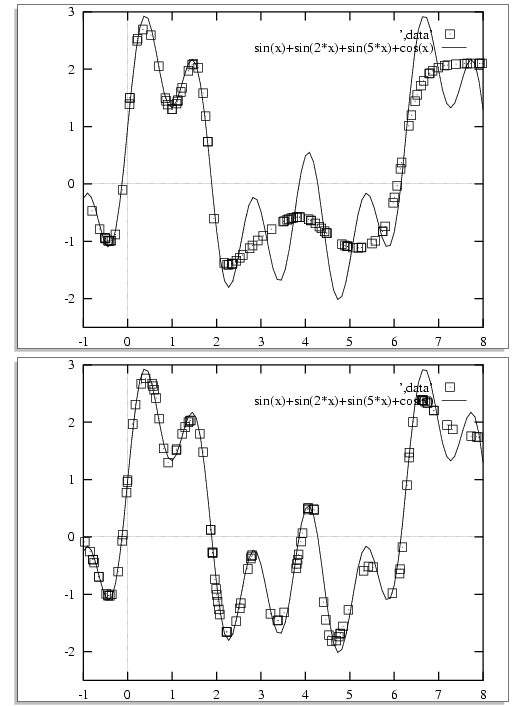
f(x) = sin(x) + sin(2x) + sin(5x) + cos(x)

Here is the kind of thing we want - a learning method approximating the above function after having seen 1 million exemplars (top) and 5 million (bottom):

See details later.

Why do examples use equation for f?

Above we considered some non-linear function f and gave an equation for it.

It is important to note: If we have an equation for f, then we don't need supervised learning or any learning. Just represent f by equation.

Supervised learning from exemplars is for situations where we have an unknown f - we simply postulate that some mapping from our inputs to our outputs must exist.

So why do we often use an explicit f, both above and below?
To show how the algorithm will work.
With explicit f, we can see how the algorithm is doing.
Use explicit f to debug your algorithm. Then release it on unknown f.

Example unknown or postulated functions

There is a learnable Input-Output relationship of some sort, but not one that can be easily expressed as an equation.

Character recognition
- Input is multi-dimensional x representing a bitmap of hand-written character.
- Output is one of 10 values (0-9) or perhaps one of 62 values (a-z, A-Z, 0-9) or more.
- One of the things that makes this problem easier is the small number of possible outputs. We do not have to know exactly that some input is a "3". We only have to decide if it is more likely to be a "3" than an "8". We have to decide which of a small number of predefined categories it is most likely to go into.
- In the input, how would you represent n x n pixels?
- See how BMP format has a pixel array plus other data.
Mapping from Input "state" to Output "behaviour".
e.g. Input state = (wall at certain angle, velocity at certain value).
Output behaviour = one of (turn left, turn right, stop, keep going).
Pattern recognition of all forms. Computer vision with simple classification job ("Is robot about to hit wall or not?") or complex classification job (Face recognition).
Anything where explicit rules are hard to come by, but correct feedback is possible to construct. Medical diagnosis. Financial prediction. Robot actions.

Discontinuous function

One worry about unknown functions:
Some mappings of Input to Output - where there is only a disjoint, discrete mapping of certain inputs to certain outputs, and in no areas any continuous (or even approximation of continuous) mapping - do not lend themselves to learning, only memorisation.

e.g. Capitals:

Human:		The capital of Ireland is Dublin.
Machine:	OK.
Human:		The capital of France is Paris.
Machine:	OK.
Human: 		What is the capital of the UK 
		(the country between Ireland and France)?
Machine:	Emm, my guess is "Dublaris".
Human:		What is the capital of Iceland?
Machine:	Emm, "Dublin"?

There may be a function in that every argument has a unique value generated for it. But it is not continuous - no interpolation is possible.

See how Chat GPT makes up information about minor historical characters based on "nearby" major historical characters.

Do we know a priori if our function f is continuous? i.e. Is there anything to learn?

Have we listed all the inputs to construct a predictable function?

Another worry about unknown functions:
f is a postulated function - a function that is assumed to exist, but whose properties are unknown (and possibly unknowable).
Imagine trying to predict horse races:

With jockey of weight 8 stone, our horse won the race.
With jockey of weight 8.5 stone, our horse lost the race.
With jockey of weight 9 stone, our horse won the race.

With jockey of weight 8.25 stone, will our horse win or lose?
With jockey of weight 8.75 stone, will our horse win or lose?

Are these the correct inputs? Are we missing some inputs? How do we know?

Probabilistic / Stochastic / Non-deterministic functions

Another worry with learning from exemplars.
Exemplars may appear to contradict each other:

If x=0, answer is 0.
If x=100, answer is 100.
If x=0, answer is 10.
If x=100, answer is 30.
If x=100, answer is 100.

May be caused by missing inputs.

Multi-dimensional functions

If input x is multi-dimensional, how do you build up this function f?
How do you represent f?

f could be a function of the series of inputs x1,x2,...,xn that led up to the current input xn, rather than just a function of the immediate input xn.