Sigmoid activation function

For multi-layer networks, we are going to change the node model from threshold, and fire/not fire to have continuous output.
We can do this with the sigmoid function.
This has some nice properties that help us develop a learning algorithm.

Other activation functions

It is important to note that other activation functions are probably more commonly used now.
The sigmoid function makes the maths easier, but it has some properties that can slow and inhibit learning, especially in large networks.
The simple Rectifier function is more suited for large networks and is probably more commonly used now.
As we shall see, learning in networks is only a heuristic anyway. So changing the activation function and breaking the nice maths is not really a problem. It is all just a heuristic, to be tested empirically.
But the maths is nice with the sigmoid function, so let us continue with it.

Sigmoid function

Given Summed Input:

x =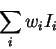

The node produces output y according to the sigmoid function:

Note e and its properties.
As x goes to minus infinity, y goes to 0 (tends not to fire).
As x goes to infinity, y goes to 1 (tends to fire):
At x=0, y=1/2

More threshold-like

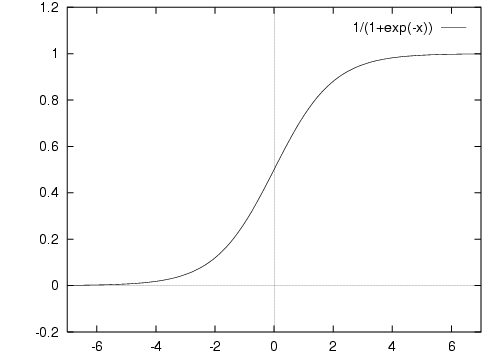
We can make this more and more threshold-like, or step-like, by increasing the weights on the links, and so increasing the summed input:

More linear

Q. How do we make it less step-like (more linear)?

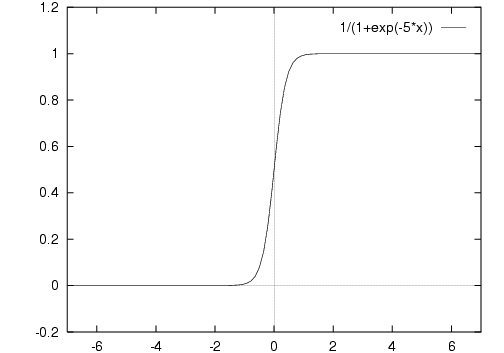
For any non-zero w, no matter how close to 0, ς(wx) will eventually be asymptotic to the lines y=0 and y=1.

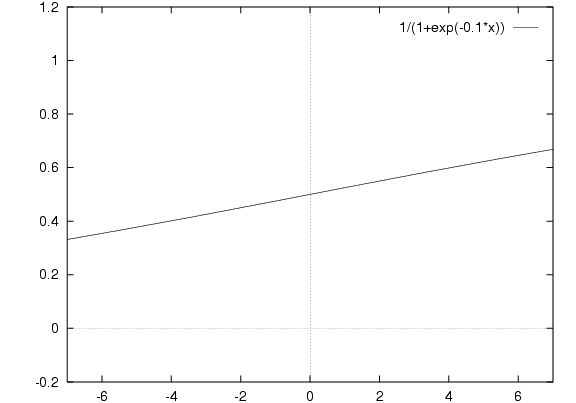
Is this linear? Let's change the scale:

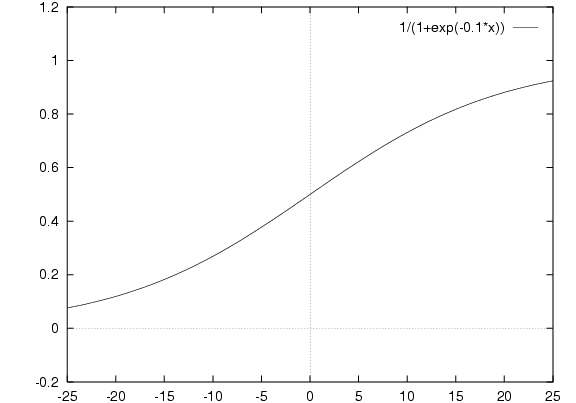
This is exactly same function.

So it's not actually linear, but note that within the range -6 to 6 we can approximate a linear function with slope.
If x will always be within that range then for all practical purposes we have linear output with slope.

Change sign

We can also, by changing the sign of the weights, make large positive actual input lead to large negative summed input and hence no fire, and large negative actual input lead to fire.

Not centred on zero

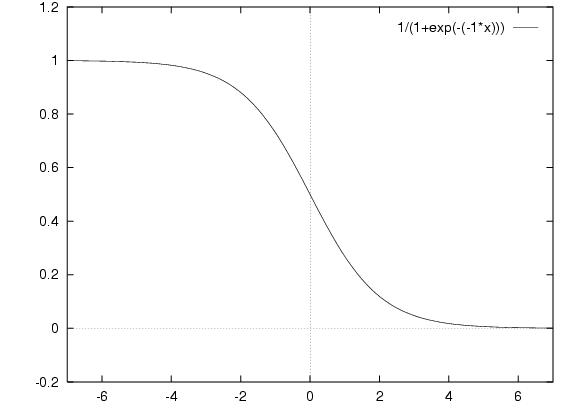
This is of course a threshold-like function still centred on zero. To centre it on any threshold we use:

y = ς(x-t)

where t is the threshold for this node. This threshold value is something that is learnt, along with the weights.

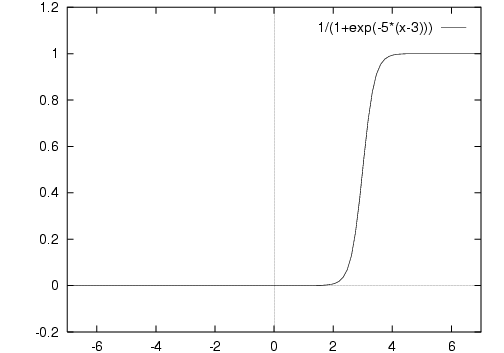
The "threshold" is now the centre point of the curve, rather than an all-or-nothing value.

General case

General case:

y = ς(ax+b)

Can we have linear output?

Can y be linear?
Yes in one way.
Set a=0
y=ς(b) = constant for all x

By varying b, we can have constant output y=c (slope zero) for any c between 0 and 1.

Cannot be linear with non-zero slope.

Properties of the sigmoid function

Back to the "vanilla" sigmoid function:

We are going to differentiate it to look at some properties.

Reminder - differentiation rules:

Product Rule:

d/dx (fg) = f (dg/dx) + g (df/dx)

Quotient Rule:

d/dx (f/g) = ( g (df/dx) - f (dg/dx) ) / g²

Max/min value of slope

Slope = y (1-y)
The slope is greatest where? And least where?

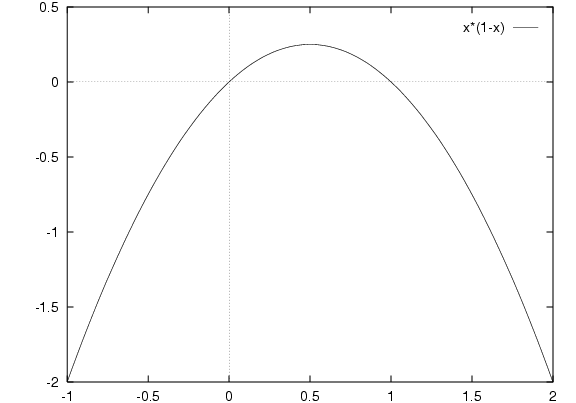
To prove this, take the next derivative and look for where it equals 0:

d/dy ( y (1-y) )
= y (-1) + (1-y) 1
= -y + 1 -y
= 1 - 2y
= 0 for y = 1/2
This is a maximum. There is no minimum.

Slope of ς(ax+b)

For the general case:

y = ς(ax+b)

a positive or negative, fraction or multiple
b positive or negative

y = ς(z) where z = ax+b
dy/dx = dy/dz dz/dx
= y(1-y) a
if a positive, all slopes are positive, steepest slope (highest positive slope) is at y = 1/2
if a negative, all slopes are negative, steepest slope (lowest negative slope) is at y = 1/2

i.e. Slope is different value, but still steepest at y = 1/2