Let D be updated by:
where d is bounded by 
, 
,
and the initial value of
.
Then:
Proof:
The highest D can be is if it is always updated with :
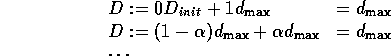
so 
.
Similarly
.
I should note this only works if
α
is between 0 and 1.
Proof: In the discrete case, Q is updated by:
so by Theorem B.1:
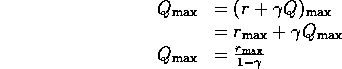
This can also be viewed in terms of temporal discounting:
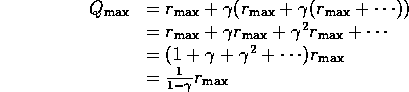
Similarly:
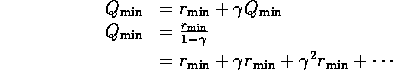
For example, if 
, then 
.
And (assuming 
) as 
, 
.
Note that since 
, it follows that 
.
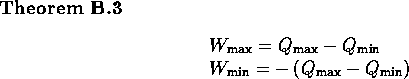
Proof: In the discrete case, W is updated by:
so by Theorem B.1:
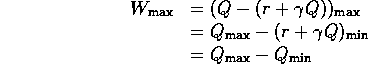
by Theorem B.2.
Similarly:
Note that since , it follows that 
.
Return to Contents page.
