Supervised learning in practice
This section explains
Supervised Learning in practice with
neural networks
and Back-propagation.
We have defined the Back-propagation algorithm.
But there is still a lot of work for the human to do in making this work.
The whole point of learning is
not to design the network.
However this is only true for not designing weights and thresholds.
There are still many design decisions.
For example:
- What input data to send to the network.
If inputs are missing, it can only learn a crude function.
- Designing the input nodes format and number of input nodes.
- Number of hidden nodes / hidden layers.
- Designing the output nodes format and number of output nodes.
Limit to what the network can represent
A neural net is an
approximation of a non-linear continuous function.
How good that approximation is, or even
can be,
will be constrained by the architecture of the network.
Backprop can't do everything.
e.g. For
the function:
f(x) = sin(x) + sin(2x) + sin(5x) + cos(x)
you can't design
a network
with 1 input, 1 hidden unit, 1 output,
and expect backprop to finish the job.
There is only so much such a network can represent.
So should you just have thousands
of hidden units?
That would tend towards a lookup table
with limited generalisation properties.
We could consider a plan:
- If too much interference (can't form representation)
increase number of hidden units
- If too little interference (can't predict new input)
reduce number of hidden units
The problem is both look the same! Lots of errors.
So we may try both increasing and reducing to see if either helps.
Design of the input node scheme (how many nodes and what values they take)
is crucial to making the network work.
The network needs to be able to separate
certain areas of the input space from other areas.
A lot of work may have to be put into clever coding of the inputs
to help the network do this.
Example of designing the inputs
Imagine that the inputs to a network are:
1 input takes integer values 0 .. 9
1 input takes integer values 0 .. 9
1 input takes integer values 0 .. 9
1 input takes integer values 0 .. 8
1 input takes value 0 or 1
Number of unique inputs = 10 x 10 x 10 x 9 x 2 = 18,000.
Possible input schemes:
- 1 input node taking values 1 to 18,000.
- 5 input nodes, each taking values 0 to 9.
- 15 input nodes, each 0 or 1 (encoding the values 1 to 18,000 in binary).
- Some more separation of inputs. Think of the order of 50 to 200 input nodes under some separation scheme.
- 18,000 input nodes, each 0 or 1.
Will the input scheme work?
- Massive interference. Won't work.
- Massive interference. Won't work.
- Massive interference. Won't work.
- A working input scheme would be somewhere in here.
- Works, but is a lookup table. No point to having a neural network.
Usually, without the right coding of the inputs, the network will not work at all.
One scheme that could work in the "sweet spot" is
One-hot encoding
(also called 1-of-N or
"1-of-C" encoding).
Example of separating the inputs:
It does seem strange that, having been told the correct answer for x,
we do not simply return this answer exactly
anytime we see x in the future.
Yes, we need a prediction machine that can generate a guess
for unseen inputs.
But how about inputs we saw before?
Why "forget" anything that we once knew?
Surely forgetting things is simply a disadvantage.
We could
have an extra lookup table on the side,
to store the results of every input about which
we knew the exact output,
and only consult the network for new, unseen input.
The question is:
- Computational cost of comparing current input with all past exemplars.
- Pointless if current input is almost always different to past exemplars.
Example
Consider
Input = continuous real numbers in robot senses.
Angle = 250.432 degrees, Angle = 250.441 degrees, etc.
Consider when n dimensions.
To see same input twice, need every dimension to be the same, to 3 decimal places.
Never happens.
If exact same input never seen twice,
our lookup-table
grows forever (not finite-size data structure)
and is never used.
Even if it is (rarely) used, consider computational cost
of searching it.
-
We could ensure that inputs are seen multiple times
by making the input space more
coarse-grained,
e.g. Angle is one of N, S, E or W.
But this of course pre-judges how the input space
should be broken up, which is exactly the job
the neural net is trying to solve!
-
In fact, even the decision to cut to 3 decimal places
(a decision probably made by the robot sensor manufacturer)
is already an a priori classification.
-
We can't actually have real numbers
in real-world engineering.
Even in software only, floating point numbers have a finite no. of
decimal places.
-
Another problem with lookup tables for inputs seen before
- exemplars may contradict each other,
especially if they come from the real world.
See over time two different Input-Output exemplar pairs (x,y) and (x,z).
Presented with x.
Do you return y or z?
Learning to divide up the input space (rather than pre-defined)
The neural network solves the problem of making the input coarse-grained or fine-grained.
In the above, if the feedback the neural net gets is the same
in the area 240 - 260 degrees,
then it will develop weights and thresholds so that any
continuous value in this zone generates roughly the same output.
On the other hand, if it receives
different feedback in the zone around 245 - 255 degrees
than outside that zone, then it will develop weights
that lead to a (perhaps steep) threshold being crossed at 245,
and one type of output generated,
and another threshold being crossed at 255,
and another type of output generated.
The network can learn to classify any area of the
multi-dimensional input space in this way.
This is especially useful for:
- (a) Where we do not know how to sub-divide the input space in advance.
- (b) Especially where the input space is multi-dimensional.
Humans are good at dividing up 1-dimensional space,
but bad at visualising divisions in n-dimensional space.
Each zone can generate completely different outputs.
Network starts with random values and learns to
get rid of these.
But that means it can learn to get rid of good
values over time.
If it doesn't see an exemplar for a while,
it will "forget" it.
Meaning weights move in a different direction.
For all it knows, it has just started learning,
and the weights it has now are just a random initialisation.
Learning = Forgetting!
Extreme Case:
We show it one exemplar repeatedly:
- Show it "Input x leads to Output 1",
a million times in a row.
-
The "laziest" way for the network to represent this
is to send weights to infinity
so Output = 1 no matter what the Input.
- Instead of "x -> 1"
it learns "* -> 1"
It needs to learn "non x" leads to "non y".
- If we show it
"x -> 1" once,
then it may have an effect on many or all weights.
- The backprop will make a tiny push of some or much
of the network towards "* -> 1"
-
But this effect is countered by the effects
of other exemplars,
pushing weights in different directions.
-
The way the network resolves this tension
is by specialisation,
where some weights are close to (or actually) irrelevant
in some areas of the input space.
Since they have little effect on the error,
backprop ensures they are hardly modified.
- Over-fitting.
When it has learnt the training set, but cannot predict for inputs outside of training set.
- e.g. Imagine only one training exemplar! Like the extreme case above.
Obviously too few exemplars.
- The over-fitting problem relates to:
- Design of training set.
- Size of training set.
- Coverage of possible input space.
-
In what order we show them.
- Train with n exemplars.
Test with a different m exemplars.
- 11 famous AI disasters, CIO Magazine, Aug 7, 2025.
- "AI algorithms identify everything but COVID-19".
"Driggs' group found their own model was flawed because it was trained on a data set that included scans of patients that were lying down while scanned, and patients who were standing up. The patients who were lying down were much more likely to be seriously ill,
so the algorithm learned to identify COVID risk based on the position of the person in the scan."
How does the process of specialising work?
- As the net learns,
it finds that for each weight,
the weight has more effect
on E for some exemplars than others.
It is modified more as a result of
the backprop from those exemplars,
making it even more influential on them in the future,
and making the backprop from other exemplars
progressively less important.
First, exemplars should have a broad spread.
Show it "x -> y" alright,
but if you want it to learn that some things
do not lead to y
you must show it explicitly that "(NOT x) -> (NOT y)".
e.g. In learning behaviour,
some actions lead to good things happening,
some to bad things,
but most actions lead to nothing happening.
If we only show it exemplars where something happened,
it will predict that everything leads to something happening,
good or bad.
We must show it the "noise" as well.
How do we make sure it learns and doesn't forget?
- If exemplars come from training set,
we just make sure we keep re-showing it old exemplars.
But exemplars may come from the world.
So it forgets old and rare experiences.
One solution is to have learning rate C decline over time.
But then it doesn't learn new experiences.
Possible solution if exemplars come from world
is internal memory and replay
of old experiences.
Not remembering exemplars as lookup table,
but remembering them to repeatedly push through network.
But same question as before
- Does the list grow forever?
Let us test the neural network with a
known function to see how it does.
Consider the function:
f(x) = sin(x) + sin(2x) + sin(5x) + cos(x)
The following uses the
C++ code for
neural network as function approximator.
1 real input, n hidden, 1 real output.
Never sees the same exemplar twice!
The network
after having seen
1 million exemplars (top)
and 5 million (bottom):
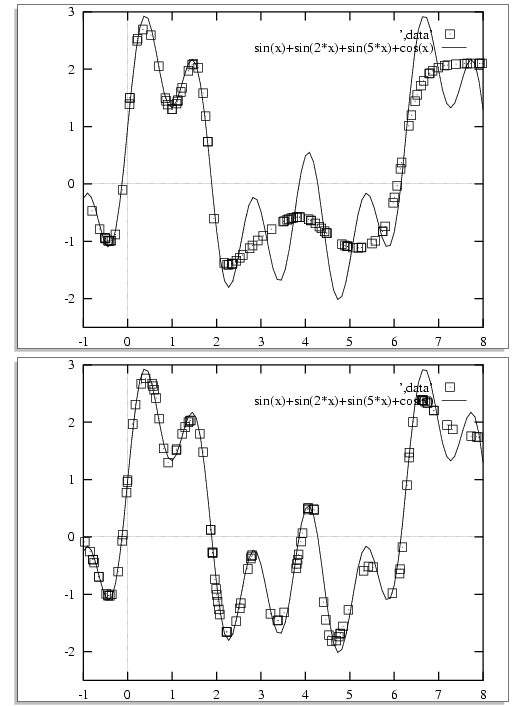
The learner of this function
was an initially-random neural network
with 1 input,
12 hidden units, and 1 output.
It improved over time, but is still not great. Why?
The reason why it has difficulty representing f
is because
there are too few hidden units,
so it can only form a crude representation.
Remember the network has not increased in size to store this
more accurate representation.
It still has just 12 hidden units.
It has merely adjusted its weights.
