Research - PhD - Chapter 11 - Chapter 12

12 Collective methods

For completeness we now describe various Collective methods, though they have not been tested. As will be discussed, we don't expect these Collective methods to perform better, but it is still instructive to compare them with the singular methods.

12.1 Maximize Collective Happiness

First, if the global reward is roughly the sum of the agents' rewards, maybe we should explicitly maximize collective rewards. If the agents share the same suite of actions, we can calculate:

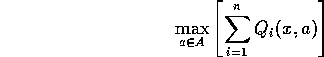
displaymath8455

Note that this may produce compromise actions. The winning action may be an action that none of the agents would have suggested. In economics, this method would be equivalent to the classic utilitarian social welfare function [Varian, 1993, §30] (the greatest happiness for the greatest number).

If the agents don't share the same suite of actions, it's hard to see what we can do. We can't predict the happiness of other agents if one agent's action is taken. We can only try it and observe what happens. This leads to the following method.

12.2 Collective W-learning (Minimize Collective Unhappiness)

The counterpart of the above is:

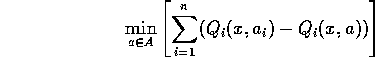
displaymath8457

That is, if agents share the same set of actions. We call this pure Minimize Collective Unhappiness.

If agents don't share the same actions, we can approximate this by a process we will call Collective W-learning. Each agent builds up a value which is the sum of the suffering it causes all the other agents when it is being obeyed. We look for the smallest . Like W-learning, agents observe and y, and build up their deficits over time. We only update the leader . In pseudocode, the Collective W-learning method is, each time step:

The change of means that there might be a different lowest W next time round in state x, and so on. As with the W-values in singular W-learning, .

Remember that in singular W-learning, we don't mind if an agent never experiences the lead because agents outside the lead are still being updated, and it obviously hasn't taken the lead because its W-value isn't strong enough. In Collective W-learning, on the other hand, we do want every agent to experience the lead since that's the only way we get any estimate of the W-value.

12.2.1 Strict lowest W

Because we update the leader's W-value only, there is again a problem with initialisation of W-values. In singular W-learning, if an agent has a high initial W-value, it wins for no good reason. In Collective W-learning, if an agent has a high initial W-value, it never gets to try being the leader, for no good reason. If all agents except one have unluckily high, positive, initial W-values, the leader converges to its true W-value somewhere lower and wins for no good reason.

So for different reasons, we have the same initialisation strategy for both - start with all zero or random negative.

12.2.2 Stochastic lowest W

Alternatively, as in singular W-learning, we could avoid the initialisation strategy by choosing the winner stochastically. Here this is the lowest W we choose stochastically. To be precise, when we observe state x, we obey agent with probability:

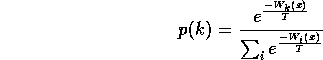
displaymath8477

Note that .

12.2.3 Collective W-learning with subspaces

Consider the plug-seeking agent , building up a W-value , of the total deficits it causes other agents when it is obeyed when the plug is in direction 5 and it moves in direction 5. What would this total deficit be? It would just be the average deficit over all states for the other agents of taking action 5, which is likely to be meaningless. It is a far cruder form of competition even than W-learning with subspaces.

Collective W-learning needs the W-values to refer to the full space to work.

12.2.4 Negotiated Collective W-learning

If agents do share common actions, we can do an instant "Negotiated" version rather than waiting for W-values to build up over time. In pseudocode, the Negotiated Collective W-learning method is, each time step:

But this would not really have any advantages over the pure Minimize Collective Unhappiness. This leads to the question of can we replace Negotiated W-learning itself by a pure Minimize the Worst Unhappiness, which we shall ask in §13.

12.3 Expected performance of Collective methods

We expect that any collective method will generate a similar sort of behavior - keeping the majority of agents happy at the expense perhaps of a small minority. Collective approaches are probably a bad idea if there are a large number of agents. The creature will choose safe options, and no one agent will be able to persuade it to take risks. Even if one agent is facing a non-recoverable state (where if it is not obeyed now, it cannot ever recover and reach its goal in the future), it may still not be able to overcome the opinion of the majority. Consider how Maximize Collective Happiness deals with this:

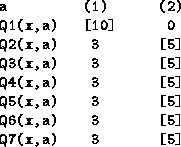
singlespace1886

This is a crucial state for agent . To get such a big difference between its Q-values this must be a non-recoverable state. If it could take action (2) and then return to this state fairly quickly its Q-value would be higher, something like:

Obviously if fails now, it can't return here easily. But Maximize Collective Happiness chooses action (2). It ends up not doing very much, giving mediocre rewards to the other 6 agents at the expense of losing the first agent, perhaps forever. It's possible that, even if the global reward is roughly the sum of the agents' rewards, Collective Happiness may still not be the best strategy, because losing means that it can't contribute to the total reward in the future. It's the whole creature equivalent of going for short-term gain even at the expense of long-term loss. At moments like this, our action selection scheme should keep on board.

As in the discussion about W=Q, we could say why not increase until tips the balance in favour of action (1). and again the answer is that this would increase all of 's Q-values, not just those in state x.

Collective W-learning (Minimize Collective Unhappiness) will give the same result as Maximize Collective Happiness here. If is in the lead, the sum . If any other agent is in the lead, its sum and it will win. Action (2) gets executed. The basic problem with a collective approach is that an individual agent must effectively beat the sum of the other agents. This is alright if its Q-values are on a different (larger) scale to theirs. But we can't have all agents' Q-values on a different scale. In W-learning, individuals only have to beat other individuals.

Finally, situations can be found which are favourable to a Collective approach. Consider this case:

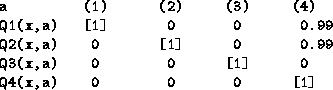
singlespace1905

Here a Collective approach is best (action (4)). If we start listening to agent , we will jump to action (3), but then other agents will start complaining and in general we risk ending up with an action that causes disaster for three agents instead of just one.

This is the question, can we allow agent , in pursuit of its action, to cause a loss less than or equal to its own for all the other agents? What may answer this question is that it is probably more likely that just one agent is facing disaster while all the others are living normally, then it is that all agents are in danger of disaster at the same time. So it will very rarely be a case of one agent dragging everyone else down with it, more likely just one agent saving itself.

In other words, situations like the above will tend not to happen. The agents' disaster zones will be spread over different states. A crucial state to one will be a humdrum state to the others. So listening to individual stories may not be a dangerous strategy.

12.4 Collective Equality

Note that maximizing the sum of happiness (or the average happiness, which is the same thing, divided by n) is not necessarily the same as spreading the happiness round lots of agents. If an agent 's Q-value is big enough it can outweigh all the others. One agent receiving 100 with nine other agents receiving zero is exactly equivalent under the Maximize Collective Happiness method to all agents receiving 10 each. If we wanted to favour the second of these, we would have to take some kind of standard deviation-based approach. For example, we could calculate:

displaymath8519

where the mean . But just minimising the standard deviation of the distribution is still not quite what we want. We don't want all Q the same if they're all going to be low.[1] Similarly for other equality measures (such as minimising the difference between the richest and poorest). We can see how in the trade off between equality and wealth in the Action Selection problem, Minimize the Worst Unhappiness is beginning to look like what we need.

[1] Continuing our economic analogy, this would presumably be communism. We may (or may not) be interested in equality at all costs in real human society - I have no interest in making statements about that. But in the Action Selection problem, it is clearly not what we want.

Chapter 13

Return to Contents page.