Research - PhD - Chapter 8 - Chapter 9

9 W=Q (Maximize the Best Happiness)

The first response to W-learning is to ask if we need such an elaborate value of W. Why not simply have actions promoted with their Q-values, as we originally suggested back in §5.3. The agent promotes its action with the same strength no matter what (if any) its competition:

and we search for an adaptive combination of 's as before. To test a particular combination of 's, we just multiply the base Q-values by them and then see how the creature performs under the rule W=Q. There are no W-values to learn.

If the agents share the same suite of actions, W=Q is equivalent to simply finding the action:

since agents suggest their best Q over a and we take the highest W=Q over i. That is, we are only interested in the best possible individual happiness. We are going to start drawing economic analogies to our various approaches. In economic theory, this would be the equivalent of a Nietzschean social welfare function [Varian, 1993, §30], where the value of an allocation depends on the welfare of the best off agent.

The counterpart of this method would be:

that is, find the action which leads to the smallest unhappiness for someone and take it. This approach is pointless because it means just obey one of the agents and cause unhappiness zero for them.

I have not seen an example of straightforward use of W=Q in Reinforcement Learning, but it can hardly be an original idea. What look like examples [Rummery and Niranjan, 1994] turn out only to be using multiple neural networks for storing Q-values in a monolithic (single reward function) Q-learning system and then letting through the action with the highest Q-value.

Searching for combinations of 's under W=Q works very well, and finds the following collection which achieves a score of 15.313. Further, the memory requirements are even less, since no W-values at all are kept.

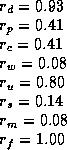
singlespace1653

9.1 Discussion

So have we wasted our time with measures of W that make compromises with the competition? Would we have been better off ignoring the competition completely?

It seems on paper that W=Q should not perform so well, since it maximizes the rewards of only one agent, while W-learning makes some attempt to maximize their collective rewards (which is roughly what the global reward is). Consider the following scenario, where there are two possible actions (1) and (2). The agents' preferred actions are highlighted:

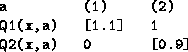
singlespace1667

If we use W=Q, then agent wins (since 1.1 > 0.9), so action (1) is executed, gets reward 1.1, and gets 0. If we use the W = (D-f) method, then wins (since it would suffer 0.9 if it didn't, while would only suffer 0.1 if disobeyed), so action (2) is executed, gets 1, and gets 0.9. If the global reward / fitness is roughly a combination of the agents' rewards, then W = (D-f) is a better strategy. In short, this is the familiar ethology problem of opportunism - can force into a small diversion from its plans to pick up along the way a goal of its own?

There's one way our W=Q search will find to solve this - by just finding a high so that it becomes:

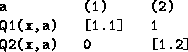
singlespace1681

But this is an unsatisfactory solution because it assumes that it is that always needs high Q-values in order for the two agents to behave opportunistically. What if in another state y, the situation is reversed and it is trying to ask for a slight diversion:

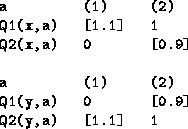
singlespace1687

Ideally we would take action (2) in both states. But W=Q will be unable to prevent action (1) being taken in at least one of the states. Currently, agent is losing state x and winning state y. We want it to win state x and lose state y. If we increase to make it win state x, we increase all Q-values across the board and make it even less likely to lose state y.

W=Q will not be able to find the opportunistic solution in cases like this, whereas W-learning will. And cases like this will be typical. Agents that ask for opportunities from other agents will themselves be asked for opportunities at other times.

In fact, any of our static measures of W, such as:

would fail to be opportunistic in situations where W-learning would be. When there are more than two actions, the other agent might not be taking the worst action for , perhaps only the second best.

So, if we agree that W-learning will find opportunism where W=Q (or any static measure) cannot, why did W-learning not perform better? The answer seems to be that the House Robot environment does not contain problems of the nature above. It contains situations where in state x, wants to slightly divert alright, but only in situations where itself doesn't mind being diverted - the 0 above becomes a 0.8. This is because all behaviors here are essentially of the form "if some feature is in some direction, then move in some direction" with rewards for arriving at the feature or losing sight of it. So if is similar to , it is because actions (1) and (2) are movements in roughly the same direction, in which case and will end up similar.

9.2 Happiness and Unhappiness

Despite its name, Minimize the Worst Unhappiness (W-learning) does not mean we're always avoiding disaster. Expected reward and expected disaster are two sides of the same coin, because if the leader is not obeyed it will be unhappy. Say we have an agent who if obeyed will gain a high reward. If not obeyed, it won't suffer a punishment, just nothing interesting happens. But it might as well be a punishment since it lost the chance of that reward. It will build up a high W-value under any (D-f) scheme.

So it would be mistaken to think that the difference between Minimize the Worst Unhappiness and Maximize the Best Happiness is that one is concerned with "Unhappiness" and the other with "Happiness". As just noted, these are really the same thing. The real difference between the two approaches is that Minimize the Worst Unhappiness consults with other agents while Maximize the Best Happiness does not consult. Minimize the Worst Unhappiness tries out other agents' actions to see how bad they are. An agent in Maximize the Best Happiness only ever considers its best action.

Chapter 10

Return to Contents page.