We assume the network will use the Sigmoid activation function.
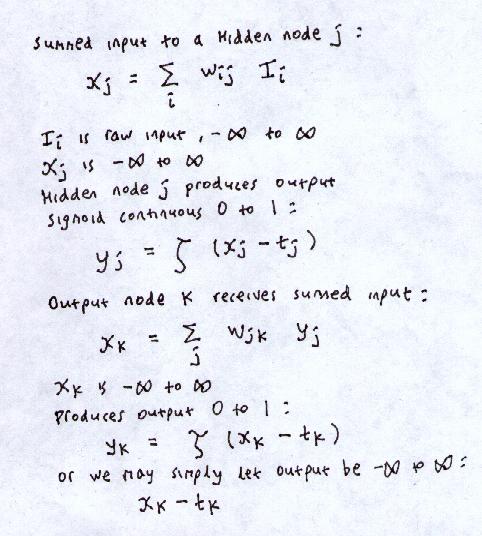
where
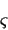 is the
sigmoid function.
is the
sigmoid function.
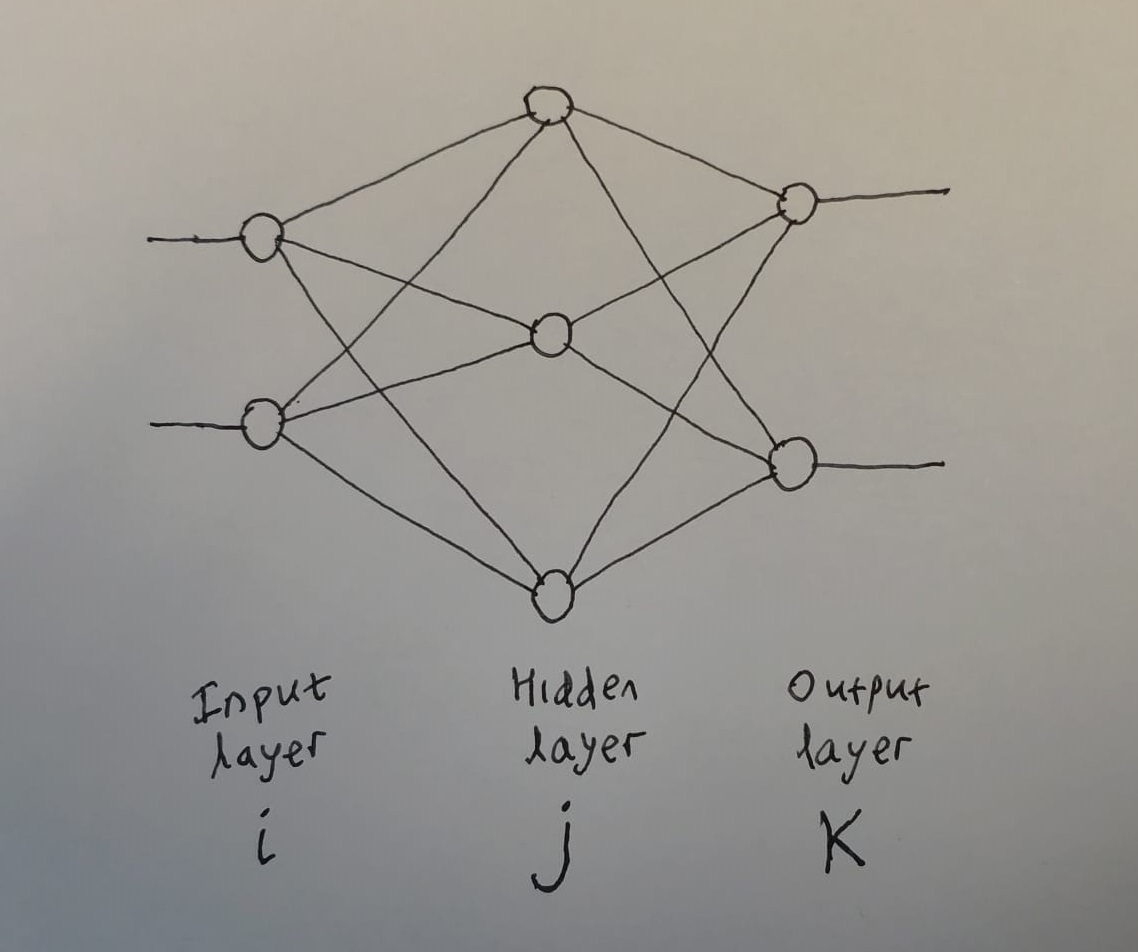
Input can be a vector.
There may be any number of hidden nodes.
Output can be a vector too.
Typically fully-connected. But remember that if a weight becomes zero, then that connection may as well not exist. Learning algorithm may learn to set one of the connection weights to zero. i.e. We start fully-connected, and learning algorithm learns to drop some connections.
To be precise, by making some of its input weights wij zero or near-zero, the hidden node decides to specialise only on certain inputs. The hidden node is then said to "represent" these set of inputs.
So we have:

and:
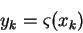
We sent in an input, and it generated, in the output nodes,
a vector of outputs yk.
The correct answer is the vector of numbers Ok.
The error term is:
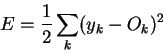
We take the squares of errors, otherwise positive and negative errors may cancel each other out.
There are other possible measures of error (recall Distance in n-dimensions) but we can agree that if this measure -> 0 then all other measures of error -> 0
Q. Prove that if this measure of E = 0 then yk = Ok for all k.
To look at how to reduce the error, we look at how the error changes as we change the weights. We start at the layer immediately before the output. Working out the effects of earlier layers will be more complex.
First we can write total error as a sum of the errors at each node k:
E = Σ k Ekwhere Ek = 1/2 (yk - Ok)2
Now note that
yk, xk and wjk
each only affect the error at one particular output node k
(they only affect Ek).
So from the point of view of these 3 variables, total error:
E = (a constant) + (error at node k)hence:
(derivative of total error E with respect to any of these 3 variables) = 0 + (derivative of error at node k)e.g.
∂E/∂yk = 0 + ∂Ek/∂ykWe can see how the error changes as yk changes, or as xk changes. But note we can't change yk or xk - at least not directly. They follow in a predetermined way from the previous inputs and weights.
But we can change wjk
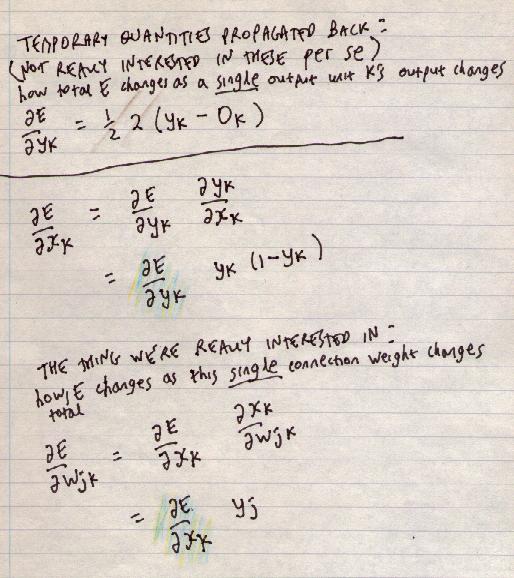
As we work backwards, the situation changes. yj feeds forward into all of the output nodes. Since:
E = (sum of errors at k)we get:
(derivative of E) = (sum of derivatives of error at k)xj and wij then only affect yj (though yj affects many things).
We can't (directly) change yj or xj
But we can change wij
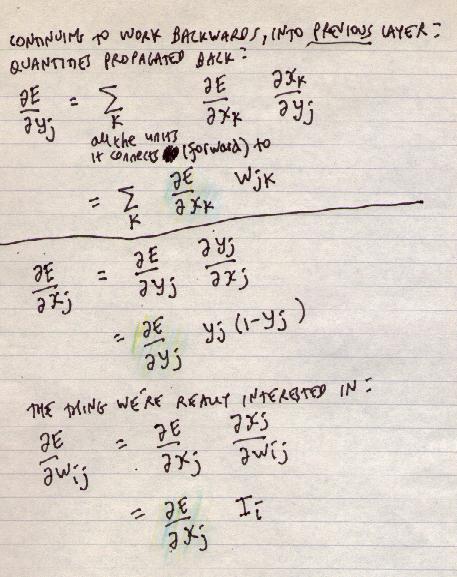
To spell it out:
∂E/∂yj
= Σ k
∂Ek/∂yj
= Σ k
∂Ek/∂xk
∂xk/∂yj
= Σ k
∂E/∂xk
∂xk/∂yj
Now we have an equation for each
 - how error changes as you change the weight.
- how error changes as you change the weight.

Note some things:
Now, to reduce error:
 > 0.
> 0.

 < 0.
< 0.

Hence the same update rule works for both
positive and negative slopes:
W := W - C
The constant C is the LEARNING RATE
C > 0
Typically
C < 1
(In the code we can try a wide range of C and see what happens.)
Remember
definition of threshold if using sigmoid function.
sigmoid(x-t)
instead of sigmoid(x)
Biasing: Just make the thresholds into weights, on a link with constant input -1.
So instead of:
we change it to:
and we just learn the thresholds like any other weights.
i.e. Every single hidden unit (and every single output unit) has an extra input line coming apparently from nowhere with constant input -1.
Remember we need thresholds, otherwise the sigmoid function is centred on zero. e.g. If no thresholds, then, no matter what the exemplars are, no matter what the I/O relationship is, and no matter what the weights are, if all inputs are 0, then output of every single hidden node is ..
Q. Is what?
Similarly, for a node that specialises on n of the inputs (weight = 0 for others), then if that subset of inputs are all 0, that node's output must be ..
 =
yk ( 1 - yk ) ( yk - Ok )
=
yk ( 1 - yk ) ( yk - Ok )
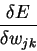 =
=
 yj
yj
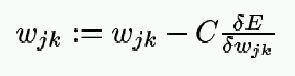
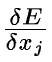 =
yj ( 1 - yj )
Σ k
(
=
yj ( 1 - yj )
Σ k
(
 wjk
)
wjk
)
 =
=
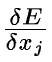 Ii
Ii

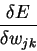 is positive,
and our learning rule reduces the weights.
This will reduce the output.
is positive,
and our learning rule reduces the weights.
This will reduce the output.