Q-learning

Recall we are trying to maximise long-term discounted reward.
Taking action a in state x yields long-term discounted reward:

Q(x,a) values

The Q-learning agent builds up Quality-values (Q-values) Q(x,a) for each pair (x,a).

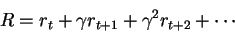
We tend to take the action with the highest Q-value:

max_b Q(x,b)

The Q-value will express the discounted reward if you take that action in that state:

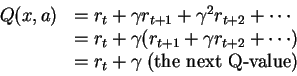
Can be built up recursively:

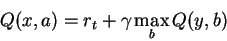
Naive attempt at a learning algorithm

You are in state x, take action a, get reward r, new state y. Then update:

Q(x,a) := r + γ max_b Q(y,b)

Problem: We allow a probabilistic world (MDP), where taking the same action a in same state x can have different results.
r may vary. y may vary.
Want to average these results instead of Q-value just expressing the most recent one.

With the above rule, the Q-value will bounce back and forth:

Q(x,a) := 5
Q(x,a) := 10
Q(x,a) := 6
...

More sensible to build up an average:

Q(x,a) := 5
Q(x,a) := 1/2 (5 + 10)
Q(x,a) := 1/3 (5 + 10 + 6)
...

How do we do this? Do we need an ever-growing memory of all past outcomes?

Building up a running average

Core Q-learning algorithm

In 1-step Q-learning, after each experience, we observe state y, receive reward r, and update:

(remember notation).

The Q-value is updated in the direction of the current sample.

Note that we are updating from the current estimate of Q(y,b) - this too is constantly changing.

If we store each Q(x,a) explicitly in lookup tables, we update:

Q-values are bounded

Since the rewards are bounded, it follows that the Q-values are bounded.

theorem3241

Proof: In the discrete case, Q is updated by:

so by Theorem B.1:

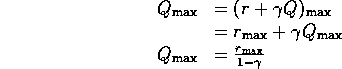
displaymath9330

This can also be viewed in terms of temporal discounting:

displaymath9331

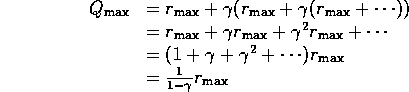
Similarly:

displaymath9332

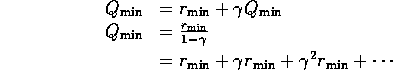
For example, if , then . And (assuming ) as , .

Note that since , it follows that .

Q_max and Q_min

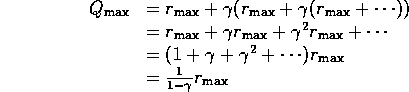
i.e. If take this action, you will get immediate reward r_max
and you can get next reward r_max (it is the best you can get in next state, other actions may be worse)
and you can get next reward r_max ..
....

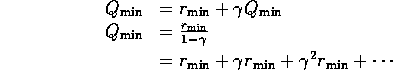
i.e. If take this action, you will get immediate reward r_min
and you have to get next reward r_min (all actions in next state lead to the worst reward r_min, otherwise the Q-value would be higher)
and you have to get next reward r_min ..
....

i.e. You are trapped in an attractor from which you cannot escape.
You cannot ever again get out and go to a state with rewards greater than r_min (and such states must exist).
Not necessarily a single absorbing state, but a family of states outside of which you can never leave.

Note if expected reward E(r) = r_min, then you will definitely get r_min on this action (r deterministic, though y can still be probabilistic).
If any reward r > r_min has non-zero probability, then E(r) > r_min

E(r) = p r_min + (1-p) r
> p r_min + (1-p) r_min
= r_min