School of Computing. Dublin City University.
Online coding site:
Ancient Brain
coders JavaScript worlds
School of Computing. Dublin City University.
Online coding site:
Ancient Brain
coders JavaScript worlds
Consider what a contrast the idea of multiple agents, with overlapping behaviors, driven by strong individuals, is to normal hand-designed systems, where task decomposition is accomplished in a parsimonious manner, with functions clearly parcelled out to different modules and a reluctance to allow any waste or overlap.
Consider the waste involved in a society of multiple competing agents solving the same problem. Or indeed, in a society of multiple agents pursuing different goals but needing to learn common skills to solve them. Where there is common functionality needed by two agents, e.g. both need to know how to lift the left leg, the normal engineering approach would be to encode this as a single function that both can call. Here in contrast, how to lift the left leg is learnt (in perhaps different ways) by both agents during development, and the information learnt is stored (perhaps redundantly) in two different places.
But recall from the discussion in §15.3.3 that just because an agent has learnt a skill doesn't mean that the agent actually wants to be obeyed. If it finds that another agent has learnt the same skill more efficiently, it will find that it does better when its own rudimentary action is not taken. Its W-values will automatically drop so that it does not compete with the more efficient agent (as long as the other agent is winning). The rudimentary skill serves no purpose except as a back-up in case of "brain damage". If the winning agent is lost or damaged, another agent will rouse itself (bring its W-values back up) to do the task (in its own slightly different way) since the task is not being done for it any more.
Instead of brittle task decomposition
we have wasteful, overlapping task decomposition.
The skill might even be distributed over a number of overlapping, winning agents,
depending on which one got ahead first in each state
(for example,
and 
in §8.2).
If one of them is lost through brain damage,
the distribution of the skill among the remaining agents shifts slightly.
Let us formalise this notion
that another agent might know better than you how to do your job.
Throughout this thesis, we have generally assumed that agents know best how to maximize their own rewards,
and therefore that their W-values are positive and they try to win.
In a Markov Decision Process, agent 
maximizes its rewards, but only relative to a particular state space, action space and reward structure 
.
These 3 things have to be designed,
and the designer might omit senses or actions that could contribute towards rewards
(as we saw in §7.1.1),
or the designed reward structure might not be rich enough to make the rewards at subgoals distinguishable from noise.
One might argue that this means the world is not really an MDP,
but the answer is that almost all complex worlds aren't MDP's anyway - we assume already
that we are just trying to approximate one.
So we have from 's point of view, there are some states x in which
it would be better for it if it let another agent 
win.
may actually have the same suite of actions as , but may for some reason be unable to learn what is doing
(e.g.
may appear to have a non-deterministic policy,
because it sees many states where
sees only one, as in §7.1.1).
In any case, if observes the average reward when wins, then it will see that it would pay on average to let it win.
Under my system, will drop out of the competition if is winning.
But if is not winning, then my model has a problem.
cannot use 's trick, whatever it is,
but has to try and compete itself,
using its less efficient strategy.
For instance, when I need to wander, ideally I give way to a highly-specialised Explore agent which does nothing else.
But if Explore isn't able to win on its own,
I have to come in with my own rudimentary version of the skill.
Digney's Nested Q-learning [Digney, 1996] shows us an alternative way, where can force to win,
even if couldn't manage to win on its own.
In the basic setup (Figure 18.1), each agent is a combination both of a normal Q-learning agent
and a Hierarchical Q-learning switch.
Each agent has its own set of actions 
and a set of actions 
where action k means "do whatever agent wants to do".
Wixson [Wixson, 1991] seems to have invented an earlier, but more restricted, form of Nested Q-learning, where the called agent is called not just to take an action for this timestep, but to take actions repeatedly from now on until its goal state is reached. Digney's model (like ours) does not demand the existence of terminating goal states. The action selection is revisited every time step. In Digney's notation the choice of possible actions is:
In our notation this would mean that we build up Q-values for J real actions plus I "actions" of calling other agents:
Each agent has its own statespace and its own actionspace.
It can learn as normal, and can also learn in a normal manner.
Every time wins state x, can update based on the state y we go to and the reward 
that is received.
It might find that in some states there is a k such that is greater than any .
Of course the difference between the agent and a Hierarchical Q-learning switch
is that the agent may not be obeyed when it says "do whatever wants to do".
It has to fight for using its own W-value 
.
The advantage of this model is that agents could specialise, and use function from other agents
without the other agent needing to be strong enough to win by its own rights.
For example, the efficient, specialised Explore agent might almost never win on its own,
but regularly win because it was being promoted by somebody else.
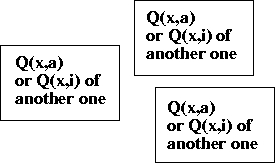
Digney's actual model is more like a hierarchy [Digney, 1996, §2.3]
with the Action Selection among the agents decided similar to a Hierarchical Q-learning switch with a global reward function.
What makes our model Nested W-learning rather than Nested Q-learning
is that we will retain the Action Selection ideas of this thesis,
while applying them to agents that are Digney's Nested Q-learners.
Here the Action Selection in Figure 18.1 would still be decided on the basis of Minimize the Worst Unhappiness. The winning agent either takes an action itself, or immediately orders someone else to take an action. But the principle of Action Selection is unchanged - the winning agent is using function from other agents for its own purposes, not for the purposes of the other agent (much as the other agent will be happy to be thus used, and will drop out of the competition if being defended by someone else's W-value).[1]
W-learning learns in effect a single value for whoever the leader happens to be.
What actual action the leader takes may seem to vary (e.g. because sees different states where sees only one)
so W-learning concentrates on just building up an average
instead of trying to find out what action(s) the leader is actually executing and building up 
values.
The agent understands what action k means, but only for a single k.
Nested W-learning learns detailed values for many other agents
and then can suggest which it would prefer to win.
Again their actions may seem to vary
so it concentrates on building up a Q-value for action k rather than for any particular real action 
.
Once all the agents have learnt such detailed values, we need to do Action Selection on these as our base Q-values.
We can now actually do pure Minimize the Worst Unhappiness, instead of W-learning,
even if agents do not share the same actions.
Because now even if does not understand action ,
it certainly understands action k.
An interesting question that arises in Figure 18.1
is whether an infinite loop could develop.
For example, normally takes action a
and 
normally takes action b.
starts to notice that b is actually better for it,
just as notices that a is actually better for it.
switches to calling
just as 's preferred action becomes to call .
At this point, if either of them wins, an infinite loop will ensue.
One solution is to choose preferred actions using only a
soft max.
Another is to design the possible Q(x,i) interactions so that a chain of commands cannot loop back on itself
(see Figure 18.3 shortly).
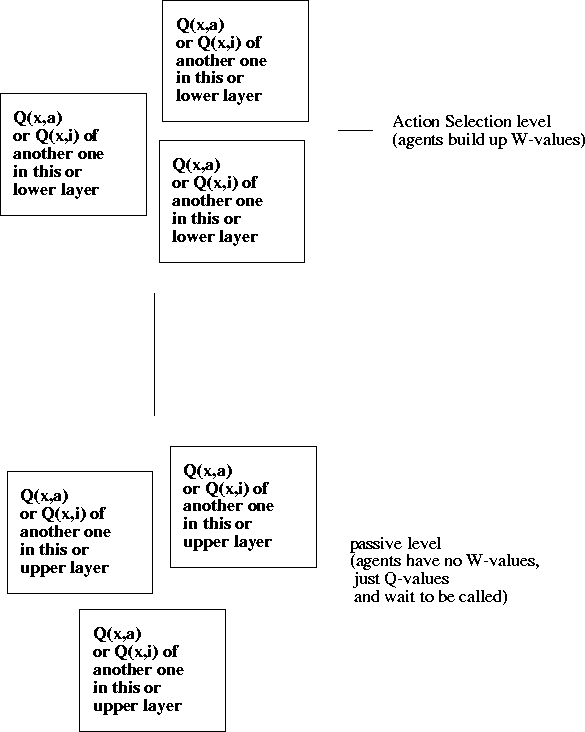
In the generic scheme (Figure 18.2) there are fundamentally two classes of agents,
those competing for Action Selection and those not.
In Figure 18.2, Action Selection takes place only among the agents in the top layer.
The lower layer agents only ever execute their actions when called by a winning top layer agent
(when called thus they simply execute their best action according to their Q-values).
For instance, in the collection of 8 agents
for the House Robot problem,
we could have 6 of them in the competitive top layer
and put 
and 
in the lower layer.
At the lower level, we have specialised Explore agents.
At the top level, we follow some goal or else call the specialised Explore.
In the generic case, agents may consist of Q(x,a) only, Q(x,i) only (the agent gets all its work done by calling other agents), or a combination of both. Note that if we take agents out of the Action Selection competition, then we only get to see what happens when they win when agents in the top layer get around to exploring different Q(x,i).
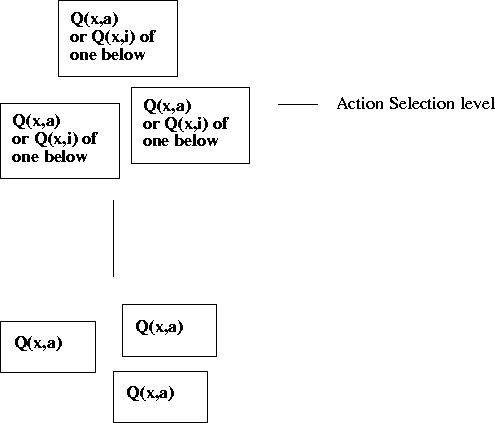
Figure 18.3: A typical form of Nested W-learning.
Figure 18.1 can now be seen to be a special case of the
generic scheme with the lower layer empty.
Another special case would be the more familiar 2-layer hierarchy
of Figure 18.3
(note that this is designed so that an infinite loop of commands is impossible).
Another special case would be to have the same agents as
in Figure 18.3
but include all of them in the Action Selection,
the (formerly-lower) Q(x,a) ones hardly ever winning on their own
(this is more like what we actually
had in §8).
The basic Hierarchical Q-learning is also just another special case,
with a single Q(x,i)-only agent in the top layer.
In a multi-layer hierarchy, agents in the Action Selection layer call agents in a lower layer, which call agents in a further lower layer, and so on. This is actually just another special case with all layers other than the Action Selection layer fitting inside the single "lower layer" of the generic case. The agents in the "lower layer" are then divided into groups with rules about which other agents an agent's Q(x,i) can refer to. The advantage of setting up such rules (apart from ensuring again that no infinite loop can occur) would be to reduce the size of i in the Q(x,i) statespace, that is, reduce the number of "useful" agents that any one agent has to know about. As we have said before though, hierarchies are only particular cases of the more general model, and not necessarily the most interesting cases either.
Watkins' Feudal Q-learning [Watkins, 1989, §9] shows another way of having agents use other agents - by sending explicit orders.
In Feudal Q-learning, a master agent sends a command to a slave agent, telling it to take the creature to some state (which the master agent may not know how to reach on its own). The slave agent receives rewards for succeeding in carrying out these orders. To formalise, the master has a current command c in operation. This actually forms part of the "state" of the slave. Using the notation (x,c),a -> (y,c), the slave will receive rewards for transitions of the form:
Note that immediately the command c changes, we jump to an entirely new state for the slave and it may start doing something entirely different.[2]
Given a slave that has learnt this, the master will learn that it can reach a state by issuing the relevant command. Using the notation x,a -> y, it will note that the following will happen:
That is, the master learns that the world has state transitions 
such that 
is high.
It then learns what actions to take based on whatever it wants to get done.
Note that it can learn a chain - that 
is high
and then 
is very high.
So the model does not fail if the slave takes a number of steps to fulfil the order.
The master may be able to have a simpler state space as a result of this delegation.
For example, in §7.1.1,
can order 
to get it to the state where it is not carrying food
(so that it can then set off for a new reward).
senses x = (i,n,c) and takes 9 move actions.
senses x = (i,f) and takes 9 move actions plus 2 command actions
(when the creature reaches the nest, will want to change the command to do nothing).
The combined state and action memory requirements of and is 544,
whereas for a monolithic sensing x = (i,n,f) and taking 9 move actions
it would be 1620.
For the W-learning agents in that section the combined state and action space was 261,
but recall that could not explicitly call
(it could only drop out of the competition and hope that would win).
Again, Action Selection must take place somewhere, and the basic principle of Action Selection is unchanged. The master is using the slave for its own purposes. The slave indeed has no purposes of its own, and so cannot be in the Action Selection loop. In Feudal W-learning (as distinct from Feudal Q-learning) Action Selection will take place between master agents on the basis of Minimize the Worst Unhappiness. The winner will either take an action itself or send a command to a slave agent.
We can combine Nested and Feudal W-learning and the Action Selection ideas of this thesis in one grand diagram showing the general form of a Society of Mind based on Reinforcement Learning (Figure 18.4). Note that this structure is not a hierarchy in any meaningful sense. While the flow of control must originate with some winner in the Action Selection layer, after that control may flow in any direction.
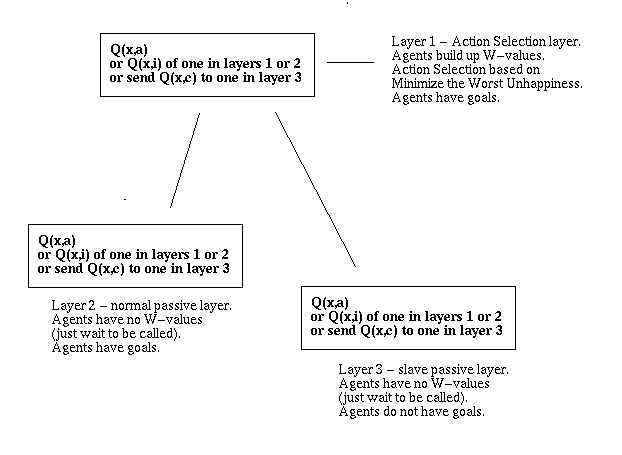
Figure 18.4: The general form of a Society of Mind based on Reinforcement Learning.
This is not a hierarchy.
Neither Nested nor Feudal approaches affect the basic analysis we made in this thesis of how Action Selection between competing peers should be resolved. The basic ideas running throughout this thesis, of overlap driven by strong individuals, of multiple unexpressed behaviors and agents dropping out of competitions, all have a parallel in Minsky's "If it's broken don't fix it, suppress it" maxim in the Society of Mind [Minsky, 1986]. In Minsky's model, the normally-good behavior is allowed expression most of the time, except in some states where a censor overrides it and prevents its expression. This would be like W-learning between a general solver of a problem and a highly-specific agent introduced to focus on one small area of statespace. The specialist remains quiet (has low W-values) for most of the statespace and only steps in (has high W-values) when the state x is in the area of interest to it.
For example, we could have specialised agents which are trained to look for disasters,
combined with a more careless agent dedicated to solving the main problem.
The main agent is allowed a free run except at the edges near to disasters,
at which the previously quiet
disaster-checkers will raise their W-values to censor it.
The looming disaster might be obvious in the disaster-checker's sensory world
but invisible in the main agent's sensory world.
We end up with one agent generally in charge,
but being "shepherded" as it goes along its route by a variety of other agents ,
who are constantly monitoring its actions and occasionally rising up to block them.
Where all this is leading is away from the simplistic idea of a single thread of control. Any complex mind should have alternative strategies constantly bubbling up, seeking attention, wanting to be given control of the body. As Dennett [Dennett, 1991] says, the Cartesian Theatre may be officially dead, but it still haunts our thinking. We should not be so afraid of multiple unexpressed behaviors:
The concept of ideas having to fight for actual expression is of course not original. The idea of competition between selfish sub-parts of the mind is at least as old as William James and Sigmund Freud. But what I have tried to do in this thesis is to provide some fully-specified and general-purpose algorithms rather than either unimplementable conceptual models or ad-hoc problem-specific architectures.
[2] Actually there is a special case where a change of command happens just as the slave fulfilled the old command. We should still reward it - it's not its fault that the state has suddenly changed to (c,d). So we should actually reward for the transition: (*,c),(*) -> (c,*)
Return to Contents page.