School of Computing. Dublin City University.
Online coding site:
Ancient Brain
coders JavaScript worlds
School of Computing. Dublin City University.
Online coding site:
Ancient Brain
coders JavaScript worlds
Before we test W-learning in the House Robot problem, we first look at an implementation of it in a simpler problem. The reason we do this is because we want to draw a map of the full statespace, showing who wins each state. In the House Robot problem, the full statespace is too big to explicitly map. It is too big even to illustrate interesting subspaces. In this simpler problem, the full space is small enough to map.
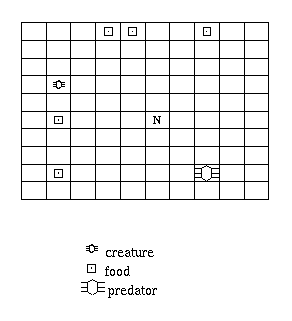
Figure 7.1: The Ant World problem.
N is the nest.
The Ant World problem is the conflict between seeking food and
avoiding moving predators on a simple toroidal gridworld
(Figure 7.1).
The world contains a nest,
a number of stationary, randomly-distributed pieces of food,
and a number of randomly-moving dumb predators.
Each timestep, the creature can move one square or stay still.
When it finds food, it picks it up.
It can only carry one piece of food at a time,
and it can only drop it at the nest.
The task for the creature is to forage food (i.e. find it, and bring it back to the nest)
while avoiding the predators.[1]
This is clearly the ancestor of the House Robot problem. The food/predators problem can be translated directly to the vacuuming/security problem - food becomes dirt, the nest becomes the plug, and the moving predators to avoid become moving family to avoid. Unlike in the House Robot problem, here the world is a proper torus, so the creature can always run away from the predator - it cannot get stuck in corners.
The creature senses x = (i,n,f,p) where:
As before, the creature takes actions a, which take values 0-7 (move in that direction) and 8 (stay still).
We searched for a good food-finding solution and a good predator-avoiding solution. See [Humphrys, 1995] for the details of what exactly our search was. The important thing here is just to show how agents can successfully interact via W-learning. The best food-finding solution was this collection of agents:
This is the collection called EVO1 in [Humphrys, 1995], rewritten to take advantage of the fact that an agent with reward function if (condition) r else s is interchangeable with one with reward function if (condition) (r-s) else 0, in the sense that both its policy and its W-values will be the same (see §C.3).
Looking at who wins each state,
wins almost the entire space where i=0 (not carrying).
In the space where i=1 (carrying), 
wins if p=9 (no predator visible).
Where a predator is visible, wins if the nest direction is along a diagonal (0,2,4,6),
otherwise the space is split between and 
.
For example, here are the owners of the area of statespace
where p=7.
The agents 
are represented by the symbols
o, NEST, pred respectively.
States which have not (yet) been visited are marked with a dotted line:
The difference between diagonals and non-diagonals was an unexpected result.
On analysis, it turned out that it was caused by
the way in which compass directions were assigned.
There are 4 diagonal directions
and 4 non-diagonal directions.
Anything which doesn't lie directly on one of the 8 primary or secondary directions
is assigned to the nearest non-diagonal direction.
So the non-diagonal directions gathered up all the messy angles
while if you sensed something on a diagonal direction you knew exactly where it was.
If the nest is sensed in a diagonal direction, then moving that way is
guaranteed to hit it without a change of direction.
If the nest is in a non-diagonal direction, then the creature may have to make
a change of direction as it moves
towards it.[2]
is more confident that it will get its reward
when it sees the nest along a diagonal and moves along that diagonal,
and it builds up higher W-values accordingly,
causing it to win these states from .
This is certainly a more subtle way for the agents to give way to each other
than a programmer would normally think of.
Drawing the complete map of the full statespace
shows that wins 49.27% of the states,
wins 34.97%
and wins 15.75%.
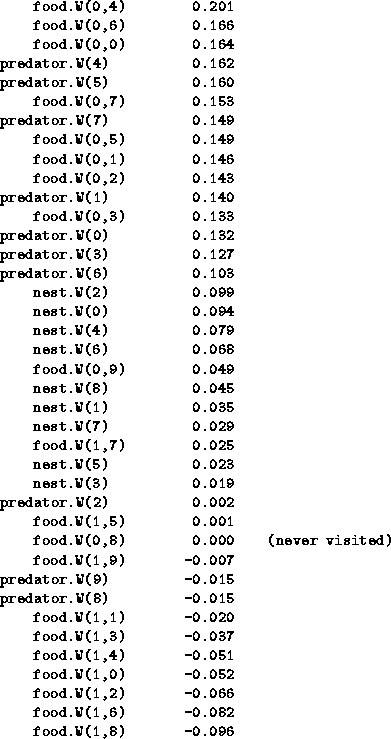
Here are all the W-values of all the agents, sorted to show who beats who.
The W-values 
are represented by
food.W(i,f), nest.W(n), predator.W(p) respectively:
The next level of analysis is what actions the creature actually ends up executing
as a result of this resolution of competition.
When not carrying food, is in charge, and it causes the creature to wander,
and then head for food when visible.
is constantly suggesting that the creature return to the nest,
but its W-values are too weak.
Then, as soon as i=1, 's W-values drop below zero,
and finds itself in charge.
As soon as it succeeds in taking the creature back to the nest, i=0
and immediately takes over again.
In this way the two agents combine to forage food, even though both
are pursuing their own agendas.
EVO1
is a good forager partly because turns out to have discovered a trick in searching for food.
In [Humphrys, 1995], I hand-coded a creature for the Ant World
(similar to the hand-coded program for the House Robot that
we saw above).
When the creature couldn't see food,
my hand-coded program just adopted the strategy of making a random move 0-7.
One might think that there is no better memoryless strategy for searching.
In fact, there is.
At any point, a diagonal move (of distance 
) reveals on average slightly more new squares
than a non-diagonal move (of distance 1).
One can see this easiest when the visible squares are simply the adjacent ones
(Figure 7.2)
but it also holds true for the distance-based field of vision we used in the Ant World.
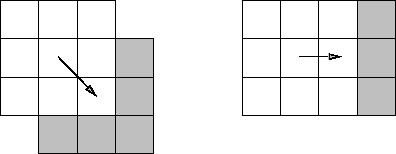
Figure 7.2: When the visible squares are simply the adjacent ones,
a diagonal move reveals new squares along two sides of the box,
whereas a non-diagonal move reveals new squares on one side only.
A diagonal move is the better search strategy.
So moving around diagonally is a better search strategy.
gradually builds up higher Q-values along the diagonals (0,2,4,6),
discovering something that might have easily escaped the programmer:
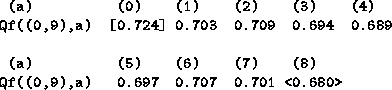
The final level of analysis is why the W-values turn out the way they do.
We can see, for example, that when i=1 (carrying food),
is a long way off from getting a reward, since it has to lose the food at the nest first.
And it cannot learn how to do this since (n) is not in its statespace.
ends up in a state of dependence on , which actually knows better than
the action that is best for it.
In our notation, regularly experiences D < f ,
and as a result the values 
here are all negative.
One can see negative W-values for the following reasons:
policy for its own reward function.
This is similar to the first point, since the agent probably needs more senses.
W can be persistently negative.
only slightly less than 
.
We have only taken a small finite number of samples, which just happen to be
from the high end of the distribution 
.
After finite time, W is negative.
After infinite time, it will end up positive.
So why not get rid of altogether
and simply supply with the space x = (i,n,f)?
Because it is more efficient
if we can use two agents with statespaces of size 20 and 9 respectively (total memory required = 29)
instead of one with a statespace of size 180 (total memory required = 180).
Obviously this only really becomes important as these numbers get larger.
As we scale up, addition (multiple agents with subspaces)
is preferable to multiplication (one agent with full space).
Here is the predator-avoiding solution:
This is the collection EVO2 in [Humphrys, 1995]. The predator-sensing agent is much stronger, and the contrast in behavior is dramatic. Here is that same area of statespace:
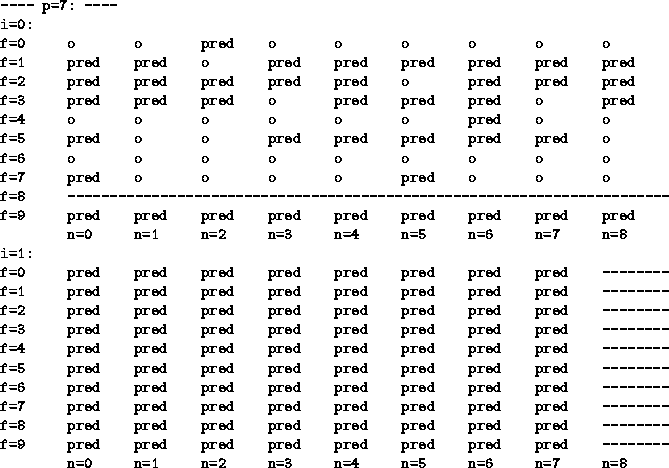
mainly dominates when a predator is visible in directions 0-7.
In particular, in that space loses the crucial state (0,9)
(not carrying food and no food visible).
In the special case p=8,
all directions are equal as far as is concerned,
and and are allowed compete to take the action.
When p=9, and fight it out as if wasn't there.
They end up combining to forage.
's share of the statespace has dropped to 35.22%,
's has dropped to 15.78%
and 's has risen to 49.01%.
Percentage of statespace owned is of course only a very rough measure
of the influence of the agent on the behavior of the creature
- ownership of a few key states may make more difference than ownership
of many rarely-visited states.
Also, we must remember that ownership of a state does not imply that the agent
had to fight other agents for it.
A weak agent may be allowed to own lots of states, but only because they
happen to coincide with what the dominant agent wants.
The ownership of all these states by the weak agent masks the fact that
the dominant agent really owns the entire statespace.
Here are all the W-values:
|
Movie demo of W-learning in the Ant World problem. |
Earlier we contrasted rewarding on transitions from x to y
with just rewarding for being in state y.
Note in the demo how rewarding on transitions makes happier to cooperate with the other agents.
It does not resist leaving the nest since it only gets rewards for the moment of arrival.
If we rewarded it continually for being in the nest,
it would resist leaving.
Similarly, does not resist being taken back to the nest and losing food,
since it only gets rewards at the moment of picking up food.
If we rewarded it continuously for having food,
it would resist going anywhere
(that is, it would try to stay still).
In general, if an agent is rewarded only for arriving at a place, once it gets there it won't stay still, but will go the minimum distance away from it and then come back so it can get the reward again. If the agent is rewarded just for being in the place, when it arrives it will stay still.
In this thesis, I leave construction of these reward functions as a design problem. Rewarding on transitions was an easy way to think about the Ant World problem, with agents "not caring" at different points, but we probably could have found a solution as well even if we rewarded continuously.
[2] For the House Robot problem, I changed this to use the nearest direction to the precise angle, so there was no bias between diagonals and non-diagonals.
[3] Problem Details - For the Movie experiment (from [Humphrys, 1995a]), when a piece of food is picked up another one grows in a random location. So at all times there are fully NOFOOD pieces on the grid. There is no such thing as "runs" - instead the world can run continuously for thousands of steps. Here SIZE=10, NOPREDATORS=1 and NOFOOD=5. Also, the nest is now only visible within a small radius (n takes values 0-9).
Return to Contents page.