School of Computing. Dublin City University.
Online coding site:
Ancient Brain
coders JavaScript worlds
School of Computing. Dublin City University.
Online coding site:
Ancient Brain
coders JavaScript worlds
Many of these action selection schemes mix together what we might call the "Q-problem" (actions to take in pursuit of a single goal) with the "W-problem" (choice between conflicting goals). Our methods rigorously separate these two different problems.
This is the same philosophy as Lorenz's "Psycho-Hydraulic" model in ethology. Lorenz's agents have a constant pressure to get executed, increasing over time. This can lead to vacuum activity - where an agent has to get expressed just because it's been frustrated for a long time, even if it is irrelevant to the current situation x. Similarly, pressure is reducing on agents that are being expressed, which may stop them even though they are not finished their task. While some animals do indeed appear to engage in vacuum activity, Tyrrell [Tyrrell, 1993] argues convincingly that vacuum activity should be seen as a flaw in any action selection scheme. Control should switch for a reason.
It is not clear anyway that time-sharing effects cannot be achieved by a suitable state representation x. If an activity goes on for long enough, some internal component of x (that is, some internal sense, e.g. "hunger") may change, leading to a new x and a potential switch in activity.
The advantage of a state-based approach is that x contains a reason why control has switched, which we can then analyse. We can discuss who is winning particular states and why, and so on. The analysis of time-based action selection seems much more complex and arbitrary.
In W-learning, control never switches without a reason grounded in the present (in the current state x).
I am unconcerned about agents being frustrated for long stretches of time,
endlessly suggesting their actions and being disappointed
(such as the nest-seeking agent
in §7.3).
It's not viewed as pain, or Lorenz's water pressure building up.
It's only information.
A classic ethology problem is: if priorities are assigned to entire activities, how does a low-priority activity ever manage to interrupt a higher-priority one? For example, the conflict between high-priority feeding and low-priority body maintenance discussed by [Blumberg, 1994]. Here is how W-learning would solve it.
The Food-seeking agent 
suggests actions with weight 
.
The Cleaning agent 
suggests actions with weight 
.
Both see the full state x = (e,f,c) where:
The sense c is irrelevant to the rewards that the Food-seeking agent receives.
Both e (whether food is visible) and f are relevant to its strategy.
We expect that 's reward function 
is a function partly of internal sense,
giving higher rewards for eating when very hungry
(consider it as a chemical rush - then it would be stronger when the creature is very hungry).
Then the W-values will work out higher when very hungry too.
We will find that for a given e, will rank its W-values:
Why would the W-values work out like this? Because if it is very hungry and eats, it gets a high reward R, otherwise zero. Hence W (the difference between the two) is high. If it is not hungry and eats, it gets a low reward r, otherwise zero. Hence W (the difference between the two) is low. Actually, because the Q-values represent a discounted look at future steps, the situation will be slightly more complex. It will be more like:
Q(very-hungry,eat) = R
Q(very-hungry,not-eat)(we can eat on the next step)
Q(not-hungry,eat) = r
Q(not-hungry,not-eat)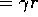
Hence:
W(very-hungry)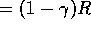
W(not-hungry)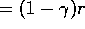
W is still higher when very hungry. Here the W-value is influenced simply by the size of the reward.
Similarly for the Cleaning agent .
Here both e and f are irrelevant to its rewards.
It can clean at any time, irrespective of what its external senses e are.
It will rank its W-values:
So how would the low-priority activity get expressed?
A very strong Food-seeker , only rarely interrupted by a Cleaner ,
would be represented by, for a given e:
in which case wins all the states (e,2,*) and (e,1,*).
wins the state (e,0,2).
And wins the states (e,0,1) and (e,0,0).
The creature only cleans itself when it is very dirty and not hungry.
Otherwise, it feeds.
The typical weak, low-priority agent only manages to raise its head in one or two extreme states x which are its very last chance before total disaster. It has been complaining all along but only at the last moment can it manage a W-value high enough to be obeyed.
Note that by feeding continuously, the state may change from (e,2,2) to (e,0,2), in which case there is a switch of control. But this switch of control has a reason - it is not fatigue with the feeding action, it is the movement into a new state x. The effect of time-based switching occurs when the state-based creature is in continuous interaction with a changing world.
Having internal hunger that increases over time does not necessarily break our MDP model.
As [Sutton, 1990a] points out,
we simply redraw the boundary between the creature and its environment.
Where x is "hungry",
y is "very hungry",
and a is "do nothing",
we might have say 
and 
for any timestep.
To enable a state-based approach to action selection, we do in fact assume that goals generally decline in urgency after they have been in charge of the creature (and thus able to satisfy themselves) for a long time. Or at least that other goals increase in urgency if not pursued for a long time. This is actually quite a weak assumption. Most problems with any potential for goal-interleaving can be made to fit into this scheme, with the reward-generation of an agent having the potential to be at least temporarily exhausted if the agent is in charge for a very long time. The need for time-based action selection (above) seems to come when behaviors can go on receiving high rewards indefinitely.
[Whitehead et al., 1993] make this explicit in their scheme, where goals are inactive (don't compete), start up at random (are activated), compete until they are fulfilled, and then fall inactive again. In this work, goals are implicitly activated and deactivated by suitable accompanying internal and external senses.
Minsky [Minsky, 1986] warns that too simple forms of state-based switching will be unable to engage in opportunistic behavior. His example is of a hungry and thirsty animal. Food is only found in the North, water in the South. The animal treks north, eats, and as soon as its hunger is only partially satisfied, thirst is now at a higher priority, so it starts the long trek south before it has satisfied its hunger. Even before it has got south, it will be starving again. One solution to this would be time-based, where agents get control for some minimum amount of time.
Again, however, time-based switching is not the only answer. As Sahota [Sahota, 1994] points out, the real problem here is having actions based only on the urgencies of the goal, independent of the current situation. Opportunistic behavior is possible with state-based switching where agents can tell the difference between situations when they are likely to get an immediate payoff and situations when they could only begin some sequence of actions which will lead to a payoff later. In Minsky's example, let the full state x = (f,w,h,t) where:
(food visible) and 
(no food visible) (water visible) and (no water visible)
The food-seeking agent presents W-values .
The water-seeking agent 
presents W-values 
.
When we can see food but no water
we would expect something like:
We start off very hungry and very thirsty.
We don't stop feeding (and start dithering) when we get down to slightly hungry.
We only stop when we get down to not hungry, and only then is able to persuade us to leave,
in the absence of visible water.
If water was visible, could have persuaded us to leave earlier with a higher W-value:
It is not just a vain hope that W-values will be organised like this.
It is in the very nature of the way we have designed them on top of Q-values.
The agents we use can tell the difference
between immediate and distant likely payoff,
and will present different W-values accordingly.
Consider how might present higher W-values when water is visible.
If water is visible, it predicts reward 1 if obeyed
and reward 
if not obeyed
(not reward 0, since even if not obeyed now, it can get it on the next step).
If no water is visible, it predicts reward if obeyed
(assume we move to a state where water is visible and we can get it on the next step)
and reward 
if not obeyed (again, we can be obeyed here on the next step):
Q(water-visible,obeyed) = 1
Q(water-visible,disobeyed)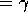
Q(no-water-visible,obeyed)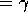
Q(no-water-visible,disobeyed)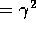
Hence:
W(water-visible)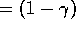
W(no-water-visible)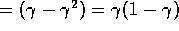
So its W-value is lower than for when water is visible. It might be very thirsty in both situations, but it presents W-values based also on whether it thinks it has a chance of satisfying its thirst. Here the W-value is influenced by how many steps away the reward is.
We see here how W-learning will support persistence,
or sticking on a goal.
When one agent 
's goal is in sight, the differences if it is not obeyed
are between immediate rather than delayed rewards.
Hence the differences between Q-values are larger (not discounted).
As its goal approaches, the agent will generate higher W-values until satisfied.
Ethologists have generally proposed positive feedback models
to explain persistence (see [McFarland, 1989, §1]),
where the strength 
of the feeding agent is being increased
by the act of feeding itself
(while at the same time being decreased by the reduction in hunger,
so that it is still probably decreasing overall).
The above analysis shows that such a time-based mechanism is not necessary
to explain persistent behavior at least.
A state-based explanation is also possible.
The fact that we are eating means that food exists close by,
and it will be easy (probably) to eat some more in the next few immediate timesteps.
Other goals may be a number of timesteps away from fulfilment.
Persistence happens because even though rewards are low, they are close by.
Note that our persistence mechanism, where W-values increase as the goal is approached, can also be seen as a positive feedback process (since being obeyed makes you even more likely to be obeyed on the next step, when you will have even higher W-values), but it is a different type of positive feedback process, state-based rather than time-based.
Our method factors in what McFarland [McFarland, 1989] calls the cost of switching from one activity to another, where nothing useful may happen for some time. Here, the Q-values are a promise of what will happen in the future, suitably discounted, and the W-value scheme makes an action selection decision based on the different agents' promises. High rewards far away may compete against low rewards close by.
Looking closer at McFarland's work, a W-value can be seen as equivalent to the "tendency" to perform a behavior in his model of motivational competition [McFarland, 1989].
His motivational isoclines are contour lines
on a map of the state space
(similar to Figure 5.6
but for a single agent
),
joining together states 
whose W-values are equal: 
In his model,
the continuous performance of an activity traces a trajectory through the statespace,
which may cross isoclines,
leading to a switch of behavior.
That is, performing an activity may cause us to enter a new state x
in which there is a new winner
and hence a switch of behavior.
Note that my model does not assume the trajectory has to be continuous
- we may make leaps from point to point in the statespace.
First, by hierarchical models we mean multi-level systems where the modules are built into some kind of structure. Some modules have precedence over others, and control flows down to their submodules. While many problems seem to lend themselves to this kind of solution, there is normally a considerable burden of hand-design. This thesis has consistently argued that there is no future in models that are not capable of some self-organisation.
Brooks' Subsumption Architecture was introduced in §5, and his ideas used as the basic inspiration for our model. A Brooks-like hierarchy would be a special case of our more general model. To implement a hierarchy, we would have strong higher level agents and weak lower ones such that when nothing is happening relevant to the higher agent, it does not compete against the lower ones but when it competes it will always win.
A hierarchy is only one of many possible ways that W-learning agents might automatically divide up control. In this problem, the best solutions were not strict hierarchies. Note also that with W-learning, a hierarchy may form only temporarily at run-time, and be dissipated when new agents are created that disrupt the existing competition.
Hierarchies may themselves be what Brooks [Brooks, 1991a] criticised traditional AI for - structures whose main attraction is that we find it easy to think about them. Just as we find it easier to think of central control than distributed, so we find it easier to think of hierarchies than of collections of agents that cannot be ranked in any single order. One agent sometimes forbids the other, then later vice versa.
Brooks acknowledges this to a certain extent in [Brooks, 1994, §3], but then avoids the question of who should win in a competition between peers by moving on (in the Cog project) to models of spreading excitation and inhibition through networks.
Hierarchies have also long been popular in ethology. Baerends, for example, put a great deal of work into breaking down the behaviors of the digger wasp and the herring gull into multi-level hierarchical structures. See [Tyrrell, 1993, §8] for a survey of this and Tinbergen's hierarchical models.
Nested Q-learning will be introduced in §18.1. It can be used as a hierarchical model, but that chapter shows that it can also be built into a more general scheme, of which a traditional hierarchy is only a special case.
Feudal Q-learning will be introduced in §18.2. Again, it is easy to think of it as a hierarchical scheme, but I show that that is only a special case of the more general model.
Self-organising models divide into two groups - serial (agents must terminate before other agents start) and parallel (agents endlessly interrupt each other). The Action Selection problem is essentially about the latter. Serial or sequential models have already been criticised in §3.
Singh's Compositional Q-learning [Singh, 1992] was addressed in §3.
Wixson's model (to be introduced in §18.1) is basically a serial form of Nested Q-learning, where we must wait for agents to terminate at their goal states before control may switch to a new agent.
Maes' Spreading Activation Networks [Maes, 1989, Maes, 1989a] or Behavior Networks consist of a network of agents (or nodes) which are aware of their preconditions. Nodes can be linked to from other nodes that can help to make those preconditions come true, or be inhibited by other nodes who will cause their preconditions to not hold. They can in turn link to other nodes whose preconditions their behavior can affect.
Agents in our system do not have explicit preconditions.
It's just that if we are in a state x where agent cannot take any meaningful action,
its W-value 
will be low
since there will be little difference between its Q-values whatever action is taken.
So it will in effect not compete.
Our system could also be seen as more
decentralised in the sense that agents have no explicit concept of what other agents' goals might be.
They only discover when the other agents start taking their actions.
Maes' spreading activation mechanism spreads excitation and inhibition from node to node. As in other methods, we see that the "Q-problem" and the "W-problem" are mixed together. For example, the desire to pursue a goal sends excitation to the consummatory action node, which if not executable propagates excitation back to appetitive action nodes. In this way links encode temporal appetitive-consummatory relationships between nodes. But in our system, basic Q-learning takes care of this on its own and it is not seen as part of the problem of action selection.
The advantage of mixing the "Q-problem" and the "W-problem" here is that appetitive nodes can be shared by multiple goals. But Tyrrell then shows [Tyrrell, 1993, §9.3.3] that there may be problems caused if we can't tell if the "Explore" node is excited multiple times because it is serving multiple goals or because it is serving multiple paths to the same goal. Ideally, if it was serving multiple goals, we would allow it to be highly excited, whereas if it was only serving multiple paths to the same goal we would divide its excitation by the number of paths to express that it was only serving one goal. But because we can't tell the difference at a local level, we can't define a local rule to divide up the excitation or not.
In my architecture, each goal is taken care of by a separate agent. Each has to implement its own explore. The equivalent of "Explore" serving multiple goals would be multiple agents wanting to take the same action. If an action serves multiple goals it will be defended by multiple W-values. If it serves one goal via different paths it will only be represented by one W-value.
It might seem wasteful that I make each agent implement its own "Explore" but this does not mean that each agent actually wants its "Explore" to be obeyed. All I mean is that each is a complete sensing-and-acting machine which can suggest an a for each x. If there is an efficient specialised Explore agent present, agents find they do better when their own rudimentary explore or random motion action is not taken. So they do not try to compete (as long as Explore is winning).
Say we have 5 agents, and 3 of them want to do the same thing. In Maes' scheme they would divide up their excitation but as Tyrrell points out they then can't compete on an equal footing with the other 2.
In W-learning, all 5 would initially compete all against each other. If one of the 3 starts winning the whole competition, the other two of the 3 will back off. Agents back off when someone else is fighting their battles for them, but only if they are winning.
In parallel, or Pandemonium, models we have multiple agents trying to control the body simultaneously, and some intelligent (or dumb) switch deciding which one of them (or combination of them) to let through.
Lin's Hierarchical Q-learning has already been introduced (in §3) and subsequently tested.
The ancestor of our abstract decentralised model of mind is Selfridge's Pandemonium model [Selfridge and Neisser, 1960]. This is a collection of "demons" shrieking to be listened to. The highest shriek wins. Selfridge's implementation was in the area of pattern recognition or classification, where the demons examine different features, and their weight (shriek) is the similarity of the input to the structure of the demon. For example, each demon might be a character-recogniser. Demons' weights might be hand-coded, or they might be learnt by Supervised Learning. When the correct output is given, weights could be strengthened or weakened.
While there are many descendants of this kind of model in pattern recognition, it is not clear how it translates to the Action Selection problem, where demons become control programs, suggesting actions to execute, each pursuing different goals. What should the weights represent? Similarity to what? What is the "correct" demon? How should the weights change?
The Competitive Learning algorithm, an unsupervised learning technique in connectionism, can be seen as a detailed implementation of a pandemonium model.
In a neural network, the input pattern must be somehow encoded in the weights on the links leading into the hidden layer. Normally one finds that the representation is spread over a number of hidden units cooperating. In Competitive Learning, a single hidden unit will represent the input pattern. Given a particular input, a large number of hidden units compete to represent it. The winner is the one whose incoming weights are most similar to the input. The winner then modifies its weights to be even more similar to the input. We do not (as we normally would) modify the weights of all hidden units, only those of the winner.
In this way, each hidden unit ends up winning a different cluster of input patterns and its incoming weights converge to the centre of the cluster.
Again though, while a detailed implementation is useful, this is still directed towards the pattern recognition or category formation problem. It hasn't answered the question of how to apply this to Action Selection.
Jackson [Jackson, 1987] attempts to apply a pandemonium model to Action Selection. He has demons taking actions on a playing field, forging links with successor demons in the stands by exciting them, to get temporal chains of demons.
This is partly temporal chains of actions, which we saw is taken care of in pursuit of a single goal by basic Q-learning. It is also partly temporal sequencing of agents, or time-based action selection, that I criticised above. As we can see, the "Q-problem" and the "W-problem" are mixed together here.
Jackson's paper is full of interesting ideas but it is a conceptual model so it is hard to know whether it would really work as claimed. It would be interesting to see a model detailed enough for implementation.
The Distributed Architecture for Mobile Navigation or "DAMN" architecture [Rosenblatt, 1995, Rosenblatt and Thorpe, 1995] is a pandemonium-like model for Action Selection. Agents vote for actions, and the action which receives the most votes is executed. The action selection method is similar to Maximize Collective Happiness. Agents must share the same suite of actions, and be able to provide votes for actions other than their first choice. To find the best action to execute, the creature calculates the equivalent of:
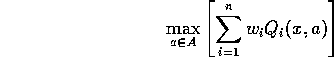
where the 
are a set of weights reflecting which agents are currently priorities of the system.
The idea is that these weights can be used to adjust the strength of an agent relative to its fellows
to avoid the pitfalls
of a collective method, such as inability to be single-minded.
But one couldn't multiply all of 's Q-values by the same weight,
as we saw earlier.
We need 
, a weight specific to the state.
Rosenblatt acknowledges this,
and suggests the weightings can be changed dynamically as the creature moves through different states x.
But he has no automatic way of generating these weights.
This is all part of the burden of hand-design.
The utility theory developed in [Rosenblatt, 1995] develops a hand-designed equivalent of a static W = importance scheme, where the agent's vote for an action is calculated relative to all alternative actions. One difference is that the agent has a vote for every action W(x,a). His normalised equation:
is the equivalent of the normalised equation:
There is a special case where the denominator is zero (all Q-values are the same) but then the numerator is zero as well. We would just set W = 0 .
The trouble with the above measure is that we are really only interested in the best Q-value, for which W(x) = 1 always. We could do a dynamic form of scaling perhaps:
but it is unclear what the advantage would be. If we multiply the Q-values by a constant, the W-value would remain unchanged. We have no easy mechanism for making agents stronger or weaker. The argument against scaling was presented in §8.1.
The Behavioral Synthesis Architecture [Aylett, 1995] is another example of hand-designed utility functions for behaviors. For example, Aylett's behavior pattern equation:
is equivalent to the agent being able to generate for any x an action and an associated utility:
The action selection is similar to Maximize Collective Happiness. Again, the difference is that these numbers are all designed by hand.
As was mentioned when it was introduced, our basic model of parallel internal competition is a form of drives model from ethology. Here the difference is we provide an answer to the question of where the drive strengths come from.
Implementing a W = D - F measure is essentially what Tyrrell is trying to do in his parameter tuning to get an implementation of drives working [Tyrrell, 1993, §9.3.1]. The amount of hand-design he needs to do only points out the value of self-organisation of these numbers.
For example, if a predator is visible he designs his "Avoid predator" drive to have a high drive strength (it must be listened to). If no predator is visible he gives it a low drive strength (it doesn't matter if it is not listened to).
When avoiding a moving predator, the predator-avoiding agent 
must be listened to precisely
(the creature must move in exactly the opposite direction).
When avoiding a stationary hazard, any action is alright so long as it isn't the one action
in the direction of the hazard.
So it doesn't matter if the hazard-avoiding agent 
is not listened to
if other agents don't want to go in that exact direction anyway.
Under W-learning, these numbers would have been built automatically.
would learn a high W-value if (as probable) other agents wanted to do anything else
other than move away from the predator.
would know that only that particular direction was bad,
and would learn a low W-value (would not compete) if other agents were going in some other direction anyway.
In [Tyrrell, 1993, §11.1.2], Tyrrell's hierarchical decision structure implements a form of Maximize the Best Happiness, while his free-flow hierarchy implements a form of Maximize Collective Happiness.
Work at the University of Rochester [Whitehead et al., 1993, Karlsson, 1997] addresses the same question as this thesis - given a collection of competing peers, who should win? Their nearest neighbor strategy is effectively Maximize the Best Happiness (W=Q). Their greatest mass strategy is Maximize Collective Happiness. A Minimize the Worst Unhappiness strategy was not tried.
[Karlsson, 1997] argues that a modular approach learns a sub-optimal policy quicker and with less memory than a monolithic approach. While this is true, I further point out that the monolithic approach may not even learn the optimal policy itself.
[Ono et al., 1996, §2], in their implementation of greatest mass, implement exactly the Maximize Collective Happiness strategy.
For completeness, I point out which category this work itself belongs to. In their basic form, W-learning and related strategies are standard, one-layer, parallel models. §18 will show how they can scale up into more complex forms of societies, still self-organising.
Finally we consider other related work which looks to be relevant but on closer examination may not be quite so relevant.
In this thesis we have agents with reward functions of the form:
if (condition) then rewardand we use a genetic algorithm to search through different combinations ofelse reward
and .
This may remind some of classifier systems [Holland, 1975],
which run genetic search on production rules
of the form:
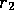
if (condition) then execute (action)The comparison is misleading. In this thesis we are not searching the space of reward function rules. We are not inventing new reward functions, only modifying the strengths of the existing ones. All we are doing is testing all different possible parameters - something any good empirical test has to do.
The classifier system rule operates at the low level of actually specifying behavior. The reward function rule operates at a higher level of specifying a value system, that must be translated into behavior. In this thesis I have been content to hand-design the reward functions and let the behavior be learnt from them. The genetic search on the reward functions' parameter values is then actually a search for different combinations of weak and strong agents. We will return to this in §17.2.
Note that classifier systems are really searching through rules of the form:
if x then execute aThey are solving the Q-problem, not the W-problem.
Grefenstette's SAMUEL system [Grefenstette, 1992] uses competition among agents, where an agent (or strategy) is a set of rules.[1] A rule is of the form: IF (condition) THEN suggest (set of actions with strengths). Hence "strength" here is the equivalent of a Q-value for the action. One difference with Q-values is that Grefenstette looks for high expected reward and a low variance in those rewards. Q-learning just looks at expected reward irrespective of variance.
"Competition among strategies" however turns out to mean only a genetic search for good strategies to solve the same problem, deleting the bad ones, and mutating good ones. There is no competition between two stategies in the same body at run-time which is what competition between agents means in this thesis. In other words, Grefenstette uses competition as a device to solve the single-goal Q-problem, rather than it being an unavoidable run-time feature of the problem, as it is in the multi-goal Action Selection W-problem.
A rule fires when its condition is met - which would seem equivalent to the rule representing the Q-values for a particular state x. An important difference though is that the conditions can be quite general, for example something like: IF fuel=[low or medium] AND speed=[600 to 800] THEN... So a rule builds up the equivalent of Q-values for actions in a region of statespace. These regions may overlap. That is why multiple rules may fire at the same time - something that cannot happen if rules are of the form IF x THEN.. where each x is a unique state. For states x lying in overlapping regions, there will be multiple estimates of Q(x,a).
Grefenstette's method of dealing with conflicting suggestions is interesting because it can be adapted for use in the Action Selection problem (which he does not address). It is a Maximize Collective Happiness strategy, but instead of summing the Q-value-equivalents, it multiplies them. His two bids (suggested actions with strengths) of:
Are combined to give a bid of:
( right(0.72),left(0.36) )
So the action "move right" is chosen for execution. This is the equivalent of having two agents with Q-values:
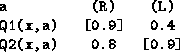
To select an action for execution, we calculate:
As before this may produce compromise actions, that none of the agents would have suggested. This method requires agents to share the same suite of actions. Note that we can't implement this method if Q-values can be negative or close to zero. Consider agents with Q-values:
Using a naive product method of Maximize Collective Happiness, action (3) will be chosen, strangely enough. Action (1) doesn't get chosen because the 0 cancels out the 0.9's. Action (4) doesn't get chosen because the -0.1 makes the product negative. And then action (3) beats action (2) because the minus signs cancel each other out.
Obviously, we must make all Q-values positive,
which is accomplished by making all rewards positive
(Theorem B.2).
Q-values arbitrarily close to zero can still cancel out an entire column,
but perhaps this is alright, since if all rewards are > 0 ,
a Q-value very close to zero means the action will not only give the agent no reward
but also take it to a state from which nothing it can do can expect to bring it a reward
for quite some time into the future.
So perhaps it is right that the agent vetoes this action.
Note that in the example above it is not good that the 0 vetoes the action
because action (1) is actually quite a good action for agent 
!
This method of Action Selection will still suffer though from the drawbacks of any collective approach, as discussed in §12.3. In a crucial state for it, one agent can get drowned out by the sheer weight of numbers of other agents, none of whom care very much about this state:
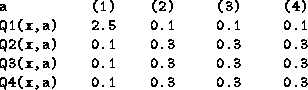
Here, agent 
is drowned out and action (1) is not taken.
Note that the summation method of Maximize Collective Happiness
would have chosen action (1) in this case.
Baum [Baum, 1996] introduces an Economy of Mind model ("A Model of Mind as a Laissez-Faire Economy of Idiots"), where new agents can be created dynamically, and agents that do not thrive die off.
An "agent" here though is simply a rule (a condition-action pair). There is a single goal, and the economy selects agents over time to find a set of rules that best satisfy that goal. That is, as with Grefenstette, competition here is a device to solve the single-goal Q-problem, rather than referring to the run-time competition of the W-problem.
There are large numbers of these simple agent-rules (in one typical run, at any given time between 20 and 250 agents were alive). Agents pay for the right to take an action (they pay the previous winner). When an action is taken only the winner receives a reward. So an agent pays to win, but then receives two payoffs - one from the action it takes, and one in the next step when it is paid off by the next winner. What it pays should be less than or equal to on average what it receives, otherwise it will eventually be bankrupted and deleted. The agent who expects to gain the largest rewards by taking its action will outbid the others.
But these bids are not analogous to W-values. They are an estimate of expected reward, used to control the entry of new rules. New agents can only enter and thrive if their estimates are more accurate. Bids are analogous to Q-values - they are a way of learning estimates of reward in pursuit of the single goal.
It would be interesting to extend Baum's model to the Action Selection problem. "Agents" do not actually have to be simple condition-action pairs. The concept of bidding and paying for actions can still be applied even when the agents are our Q-learning agents pursuing different goals. In a strict economic model, though, agents would have no interest in letting other agents take their actions for them, since they won't receive the reward if that happens. Agents wanting to do exactly the same thing will still bid against each other. And when agents want to do similar but not exactly the same things, there can be no concept of compromise. An agent either receives its full reward or nothing. The system would seem to be incapable of opportunism.
Perhaps we should relax the strict economic analogy and allow all agents to profit if one of them does good.
An interesting comparison can be made between how control switches in a W-learning creature and in an Operating System. Operating Systems implement a sort of time-based action selection, but different assumptions make OS ideas difficult to apply to our problems.
Agents get CPU time for some time slice. There is no concept of whether or not this is an appropriate state x for them to take over. Agents can be given a priority, which gets them more frequent timeslices, but still independent of x, although the concept of priority for mouse and keyboard responsive routines could be seen as a simple form of priority based on x.
There seems no way to express the loss an agent suffers by not being obeyed as being dependent on x and on who was obeyed. In an Operating System all losses are assumed the same - the agent just has to wait some time. There is also no concept that a non-winner can profit from what the winner is doing.
Another interesting comparison is with how the Ethernet [Metcalfe and Boggs, 1976] works. In an ethernet, stations only transmit when they find the Ether is silent. When multiple stations transmit at the same time, a collision occurs and they back off at different rates, so that one will be left to transmit while the others defer their transmission. When the winner is finished, the others will start up again. It has been compared to a civilized meeting where if someone wants to speak they raise their voice and everyone else quietens down.
In W-learning, agents raise their voices (W-values) to be heard, but if the lead is taken by an agent favourable to their plan of action they will be found lowering their voices again. At any moment, all agents may have low W-values, but only because they are all happy with the current leader.
For example, in our artificial world, when no interesting features of the world are visible, almost any agent with a "wander"-type behavior can take control relatively unopposed. In fact, the wander behavior may be split among a number of agents, depending stochastically on which got into the lead first in each state.
Interesting examples of competition can be set up where an agent can do well if it is selfish, but even better if it cooperates, so long as the other agents cooperate too. Such problems include the Prisoner's Dilemma.
In our model, an agent always does best when it is selfish and is normally expected only to do as well or worse when it is not obeyed. While action selection here is not exactly a zero-sum game - nonobeyed agents still collect rewards up to and sometimes equal to their highest possible - the best strategy for an agent is still always to try to be obeyed.
A more complex strategy might be if the agent accepts it can't win, but has the choice of saying who it would support to win instead. If it votes for a winner and votes are added, though, we might again run the risk of the collective methods, where sheer weight of numbers can drown out an unpopular minority opinion.
The problem of reconciling independent wills in a society is an old problem of economic and political theory. Because of different assumptions though, much of the work is not easily transferable to the Society of Mind.
In economics, utility [Varian, 1993, §4] is used as a way of ranking an agent's preferences. It can be seen as analogous to Q-values for actions. In the standard ordinal utility theory, the precise numbers are not important. What matters is only the order in which things are ranked. This is analogous to a single Q-learning agent on its own. It is interesting how difficult it often is to find such an ordering in economics. Many apparently arbitrary functions are used, once the requirement is dropped that the precise numbers be meaningful.
In cardinal utility theory some meaning is attached to the numbers. The utility of some choice can be said to be twice that of another, and so on. Here we can introduce an analog of W-values, where the difference between the Q-values is measured. We can ask the question: "You want choice A. If we force you to take choice B, how bad is that?"
Welfare theory [Varian, 1993, §30] is the branch of economics with the most relevance to this thesis. Welfare theory makes ethical judgements about what kind of economic society we want, and suggests various social welfare functions to be optimised. We have noted in the text that some of our action selection methods are equivalent to optimising the following social welfare functions:
Rawls sides with his agents, and takes note of their individual stories, out of ethical concern for their unhappiness. We side with ours not because we "care" about them (they are only parts of the mind) but because we want individual agents to have the ability, when they really need it, to raise their voices and be heard above the others.
One considerable difference between the Society of Mind and economic societies is that economic agents don't benefit from someone else's success. They won't be happy to see another win if they could have won themselves.
The problem of reconciling independent wills has also of course long been addressed by political theory, although here the focus tends to be on rights and freedoms rather than on wealth. In fact, the analogies with our systems of action selection are even stronger:
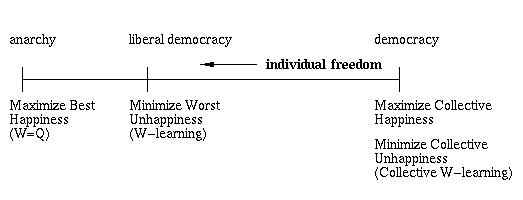
Figure 15.1: Political analogs of the action selection methods.
Note that individual freedom is not identical to individual happiness.
This is summarised in Figure 15.1.
Note that an authoritarian system would not be on this scale
since it would not involve action selection at all
- there would be a constant winner independent of state x.
In an authoritarian system, a strong agent wins all states x.
In W=Q (anarchy), strong agents win, but different ones in each x.
What is good for the Society of Mind of course may not necessarily be good for the Society of Humans, and I have no interest in making any statements about the latter. I think it would be uncontroversial though to say that, whether one is in favour of it or not, liberal democracy is a more complex idea than simple majority-rule democracy, which is perhaps why the two are often confused even in much of the democratic world.[2] Similarly in action selection, Minimize the Worst Unhappiness is a more complex idea than Maximize Collective Happiness, which is why perhaps it has been generally overlooked. In the action selection methods in this chapter, we have noted the recurring popularity of Maximize Collective Happiness schemes.
So whatever about the Society of Humans, this thesis argues that the Society of Mind (or at least our first draft of a Society of Mind) should probably be a liberal democracy.
[2] For example, in Northern Ireland "democracy" is repeatedly assumed to mean simple majority-rule democracy (with the opposing sides defining different territories over which to take the majority vote). I am not, of course, saying there is anything right or wrong with any particular model of society, but only noting that people confuse their terms.
Return to Contents page.