School of Computing. Dublin City University.
Online coding site:
Ancient Brain
coders JavaScript worlds
School of Computing. Dublin City University.
Online coding site:
Ancient Brain
coders JavaScript worlds
Looking at exactly what Q(x,i) are learnt in the previous method,
the switch learns things like
- if dirt is visible 
wins because it expects to make a good contribution to the global reward
- otherwise if the plug is visible 
wins because it expects to make a (smaller) contribution.
But the agents could have told us this themselves
with reference only to their personal rewards.
In other words, the agents could have organised themselves like this in the absence of a global reward.
In this chapter I consider how agents might organise themselves sensibly in the absence of a global reward. Watkins in his PhD [Watkins, 1989] was interested in learning methods that might plausibly take place within an animal, involving a small number of simple calculations per timestep, and so on. Similarly, I am looking for more biologically-plausible action selection, something that could plausibly self-organize in the development of a juvenile, that would not require an all-knowing homunculus. Like Watkins, I will propose methods deriving from this motivation rather than trying to copy anything seen in nature.
The starting point for this exploration of decentralised minds is Rodney Brooks' contrast in [Brooks, 1986] between the traditional, vertical AI architecture (Figure 5.1) where representations come together in a central "reasoning" area, and his horizontal subsumption architecture (Figure 5.2) where there are multiple paths from sensing to acting, and representations used by one path may not be shared by another.
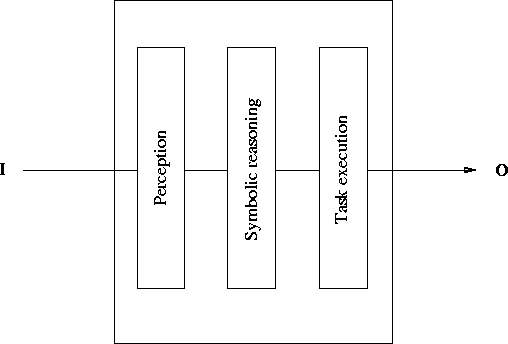
Figure 5.1: The traditional, vertical AI architecture.
The central intelligence operates at a symbolic level.
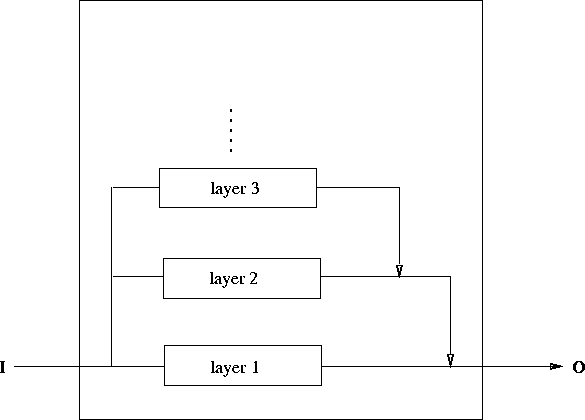
Figure 5.2: Brooks' horizontal subsumption architecture.
Brooks' method is to build full working robots at each stage.
He builds in layers: layer 1 is a simple complete working system,
layers 1-2 together form a complete, more sophisticated system,
layers 1-3 together form a complete, even more sophisticated system,
and so on.
Lower layers do not depend on the existence of higher layers,
which may be removed without problem.
Higher layers may interfere with the data flow in layers below them
- they may "use" the layers below them for their own purposes.
To be precise, each layer continuously generates output unless inhibited by a higher layer.
Subsumption is where a higher layer inhibits output by replacing it with its own signal.
If a higher layer doesn't interfere,
lower layers just run as if it wasn't there.
Brooks' model develops some interesting ideas:
The logical development of this kind of decentralisation is the model in Figure 5.3. Here, the layers (which we now call agents) have become peers, not ranked in any hierarchy. Each can function in the absence of all the others. Each agent is connected directly from senses to action and will drive the body in a pattern of behavior if left alone in it. Each is frustrated by the presence of other agents, who are trying to use the body to implement their plans. Brooks' hierarchy would be a special case of this where higher-level agents happen to always win when they compete against lower-level ones.
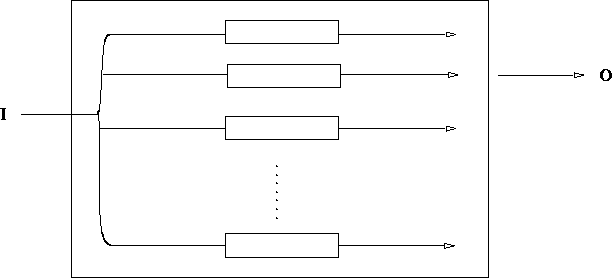
Figure 5.3: Competition among peer agents in a horizontal architecture.
Each agent suggests an action, but only one action is executed.
Which agent is obeyed changes dynamically.
This is actually the model that Lin's Hierarchical Q-learning used.
Each agent must send its actions to a switch which will either obey or refuse it.
In Hierarchical Q-learning, the switch is complex and what is sent is simple (a constant action 
).
Now we ask if we can make the switch simple, and what is sent more complex.
We ask: Rather than having a smart switch organise the agents,
Can the agents organise themselves off a dumb switch?
To answer this, I tried to look at it from an agent's point of view. Agents can't know about the global system, or the mission of the creature as a whole. Each must live in a local world. Here agents have no explicit knowledge of the existence of any other agents. Each, if you like, believes itself to be the entire nervous system.[1]
The basic model is that
when the creature observes state x,
the agents suggest their actions with numeric strengths or Weights 
(I call these W-values).
The switch in Figure 5.3 becomes a simple gate letting through the highest W-value.
To be precise, the creature contains agents 
.
In state x, each agent 
suggests an action 
.
The switch finds the winner k such that:
and the creature executes 
.
We call 
the leader in the competition for state x at the moment,
or the owner of x at the moment.
The next time x is visited there might be a different winner.
This model will work if we can find some automatic way of resolving competition so that the "right" agent wins. The basic idea is that an agent will always have an action to suggest (being a complete sensing-and-acting machine), but it will "care" some times more than others. When no predators are in sight, the "Avoid Predator" agent will continue to generate perhaps random actions, but it will make no difference to its purposes whether these actions are actually executed or not. When a predator does come into sight however, the "Avoid Predator" agent must be listened to, and given priority over the default, background agent, "Wander Around Eating Food".
For example, in Figure 5.4, when the creature is not carrying food, the "Food" agent tends to be obeyed. When the creature is carrying food, the "Hide" agent tends to be obeyed. The result is the adaptive food-foraging creature of Figure 5.5.
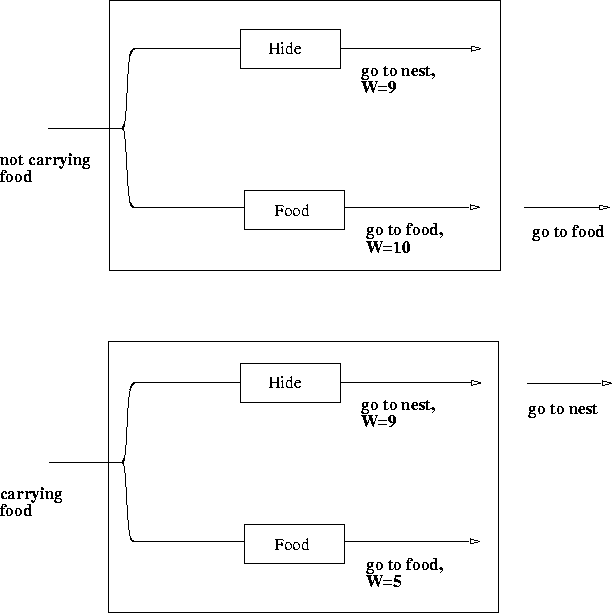
Figure 5.4: Competition is decided on the basis of W-values.
The action with the highest W-value is executed by the creature.
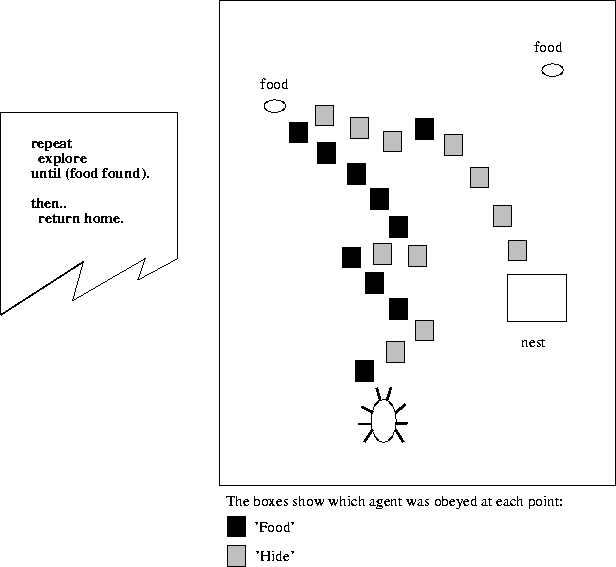
Figure 5.5:
Internal conflict, adaptive external behavior:
the conflict between the agents "Hide" and "Food" results in an adaptive food-forager.
On the left is the kind of global, serial, control program
one would normally associate with such behavior.
On the right, the two competing agents produce the same effect without global control.
Note that the
"Hide" agent goes on suggesting the same action with the same W
in all situations.
It just wants to hide all the time
- it has no idea why sometimes it is obeyed, and other times it isn't.
We can draw a map of the state-space, showing for each state x, which agent succeeds in getting its action executed. Clearly, a creature in which one agent achieves total victory (wins all states) is not very interesting. It will be no surprise what the creature's behavior will be then - it will be the behavior of the agent alone. Rather, interesting creatures are ones where the state-space is fragmented among different agents (Figure 5.6).
Figure 5.6:
We expect competition to result in fragmentation of the state-space among the different agents.
In each state x, the "Hide" agent suggests some action with weight 
,
and the "Food" agent suggests an action with weight 
.
The grey area is the area where 
.
The "Hide" agent wins all the states in this area.
The black area shows the states that the "Food" agent wins.
In fact, with the agents we will be using,
creatures entirely under the control of one agent will be quite unadaptive.
Only a collection of agents will be adaptive, not any
one on its own.
One of the advantages of Brooks' model is that layer 2, for example, does not need to re-implement its own version of the wandering skill implemented in layer 1 - it can just allow layer 1 be executed when it wants to use it. Similarly here, even though agents have their own entire plan for driving the creature (for every x they can suggest an a), they might still come to depend on each other. An agent can use another agent by learning to cede control of appropriate areas of state-space (which the other agent will take over).
Our abstract decentralised model of mind is a form of the drives model commonly used in ethology (dating back to Hull's work in the 1940s), where the "drive strength" or "importance variable" [Tyrrell, 1993] is equivalent to the W-value, and the highest one wins (the exact action of that agent is executed). Tyrrell's equation [Tyrrell, 1993, §8.1]:
is equivalent to saying that:
It is drive strength relative to the other drives that matters rather than absolute drive strength.
The big question of course is where do these drive strengths or W-values come from. Do they have to all be designed by hand? Or can they be somehow learned? Ethologists have lots of ideas for what the weights should represent, but can't come up with actual algorithms that are guaranteed to produce these kind of weights automatically. They tend to just leave it as a problem for evolution, or in our case a designer. See [Tyrrell, 1993, §4.2,§9.3.1] for the difficult design problems in actually implementing a drives model. Tyrrell has the problem of designing sensible drive strengths, relative drive strengths, and further has to design the appropriate action for each agent to execute if it wins.
It should be clear by now that we are going to use Reinforcement Learning to automatically generate these numbers. RL methods, in contrast to many forms of machine learning, build up value functions for actions. That is, an agent not only knows "what" it wants to do, it also knows "how much" it wants to do it. Traditionally, the latter are used to produce the former and are then ignored, since the agent is assumed to act alone. But the latter numbers contain useful information - they tell us how much the agent will suffer if its action is not executed (perhaps not much). They tell us which actions the agent can compromise on and which it cannot.
Systems that only know "What I want to do" find it difficult to compromise. Reinforcement Learning systems, that know "How much I want to do it", are all set up for negotiating compromises. In fact, "how much" it wants to take an action is about all the simple Q-learning agent knows - it may not even be able to explain why it wants to take it.
Our Reinforcement Learning model is also useful because given any state x at any time a state-space agent can suggest an action a - as opposed to programmed agents which will demand preconditions and also demand control for some time until they terminate. State-space agents are completely interruptable. In the terminology of [Watkins, 1989, §9], the Action Selection methods I propose in this thesis are supervisory methods, where there is a continuous stream of commands interrupting each other, rather than delegatory methods, where a top level sends a command and then is blocked waiting for some lower level loop to terminate. Watkins argues that the latter methods characterise machines (or at least, machines as traditionally conceived) while the former characterise what animals actually do.
Recently there has been an emphasis on autonomous agents as dynamical systems (e.g. [Steels, 1994]), emphasising the continuous interaction between the agent and its world such that the two cannot be meaningfully separated. It is not absolutely clear what the defining features of a dynamical system are (over and above just any self-modifying agent), but complete interruptability seems to be one part of it.
To formalise, each agent in our system will be a Q-learning agent, with its own set of Q-values 
and more importantly, with its own reward function.
Each agent will receive rewards 
from a personal distribution 
.
The distribution 
is a property of the world - it is common across all agents.
Each agent also maintains personal W-values .
Given a state x, agent suggests an action
according to some control policy,
which is most likely, as time goes on, to be such that:
The creature works as follows. Each time step:
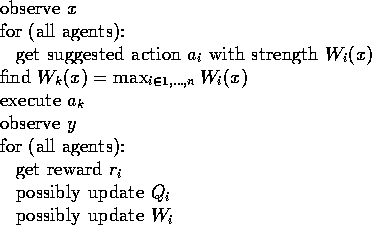
Note that the transition will generate a different reward for each agent.
For updating Q, we use normal Q-learning.
For updating W, we want somehow to make use of the numerical Q-values.
There are a number of possibilities.
A static measure of W is one where the agent promotes its action with the same strength no matter what (if any) its competition. For example:
This simple method will be the fourth method we test.
A more sophisticated static W would represent the difference between taking the action and taking other actions, i.e. how important this state is for the agent. If the agent does not win the state, some other agent will, and some other action will be taken. In an unimportant state, we may not mind if we are not obeyed. The concept of importance is illustrated in Figure 5.7.
Figure 5.7: The concept of importance.
State x is a relatively unimportant state for the agent
(no matter what action is taken, the discounted reward will be much the same).
State y is a relatively important state
(the action taken matters considerably to the discounted reward).
For example, W could be the difference between and the worst possible action:
Or W could be a Boltzmann function:
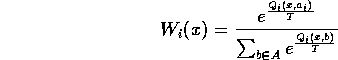
The idea of this kind of scaling is that what might be a high Q-value in one agent might not be a high Q-value to another.
A scaled measure of W could be
how many standard deviations 's Q-value is from the mean Q-value.
That is, W is the z-score.
To be precise, the mean would be:
the standard deviation would be:
and this scheme is:
If the Q-values are all the same, 
and 
.
Otherwise 
, and remember that is the best action,
so 
.
But even this measure may still be a rather crude form of competition.
Consider where there are just two actions.
Either their Q-values are the same ( 
)
or else the mean is halfway between them
and the larger one is precisely 1 standard deviation above the mean.
So to compete in a state where we care what happens,
we have 
always,
independent of the values of or the gap between the Q-values.
The real problem with a static measure of W is that it fails
to take into account what the other agents are doing.
If agent is not obeyed, the actions chosen will not be random
- they will be actions desirable to other agents.
It will depend on the particular collection what these actions are,
but they may overlap in places with its own suggested actions.
If another agent happens to be promoting the same action as ,
then does not need to be obeyed.
Or more subtly, the other agent might be suggesting an action which is almost-perfect for ,
while if 's exact action succeeded, it would be disastrous for the other agent,
which would fight it all the way.
We have two types of states that need not compete for:
's discounted reward what action is taken here.
In particular, it doesn't matter if some other agent takes an action
instead of it.
what action is taken,
but where some agent just happens to be suggesting an action
which is good for .
This may or may not be the action would itself have suggested.
With dynamic W-values, the agents observe what happened when they were not obeyed,
and then modify their values based on how bad it was,
so that next time round in state x there may be a different winner.
Imagine W as the physical strength agents transmit their signals with, each transmission using up a certain amount of energy. It would be more efficient for agents to have low W if possible, to only spend energy on the states that it has to fight for. The first naive idea was if an agent is suffering a loss it raises its W-value to try to get obeyed. But this will result in an "arms race" and all W's gradually going to infinity. The second naive idea then was let the agent that is being obeyed decrease its W-value. But then its W-value will head back down until it is not obeyed any more. There will be no resolution of competition. W-values will go up and down forever.
Clearly, we want W to head to some stable value.
And not just the same value, such as having all unobeyed agents 
.
We want the agents to not fight equally for all states.
We need something akin to an economy,
where agents have finite spending power and must choose what to spend it on.
We will have a resource (statespace),
agents competing for ownership of the resource,
caring more about some parts than others,
and with a limited ability to get their way.
What we really need to express in W is the difference between predicted reward (what is predicted if the agent is obeyed) and actual reward (what actually happened because we were not obeyed). What happens when we are not listened to depends on what the other agents are doing.
The predicted reward is D = E(d) , the expected value of the reward distribution. If we are not obeyed we will receive reward f with expected value F = E(f) . We can learn what this loss is by updating:
After repeated such updates:
Using a (D-f) algorithm, the agent learns what W is best without needing to know why. It does not need to know whether it has ended up with low W because this is Type 1 or because this is Type 2. It just concentrates on learning the right W.
Consider the case where our Q-learning agents all share the same suite of actions,
so that if another agent is taking action
we have already got an estimate of the return in 
.
Then we can directly assign the difference:
where 
and :
That is:
where 
is the deviation (expected difference between predicted and actual)
or expected loss
that causes for if it is obeyed in state x.
We can show the losses that agents will cause to other agents in a 
matrix:
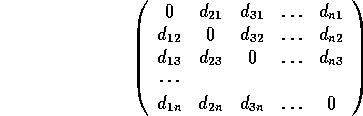
where all 
.
Note that all 
(the leader itself suffers an expected loss of zero).
Given such a matrix, can we search in some way for the "right" winner? Consider first a situation where those agents not in the lead have to raise their W-values. If one of them gets a higher W-value than the leader then it goes into the lead, and so on.
That is, there must exist at least one k such that all the values in the k'th column are less than or equal to a value in the k'th row.
Proof: The process goes:
We have a strictly increasing sequence here.
Each element is the highest in its column, so we are using up one column at a time.
So the sequence must terminate within n steps.
For a given matrix, there may be more than one possible winner. For example, consider the matrix:
Start with all 
.
Choose at random agent 
's action for execution.
Then:
Now agent 
is in the lead, and:
Agent is the winner.
However, if we had started by choosing agent 
's action, then:
Now agent is in the lead, and:
Agent is the winner.
We have a winner when somebody finds a deviation they suffer somewhere
that is worse than the deviation they cause everyone else.
We do not examine all 
combinations
and make some kind of global decision.
Rather we "walk" through the matrix and see where we stop.
Where the walk stops may depend on where it starts.
Later we will ask if we can make a global decision.
But first we consider where the only possible strategy is to make a walk.
Return to Contents page.