School of Computing. Dublin City University.
Online coding site:
Ancient Brain
coders JavaScript worlds
School of Computing. Dublin City University.
Online coding site:
Ancient Brain
coders JavaScript worlds
We do not assume in general that other agents' actions
are meaningful to an agent.
We do not assume that we have a handy estimate of 
.
If we don't, then all we can do is observe what happened when we were not obeyed
and the unrecognised action was taken.
We can observe the 
and y it led to,
and so build up a substitute for .
Now there might be many different unrecognised actions being taken by the leaders of different states.
Rather than adding them all to our action set
and learning a huge 
for every new action
for every state,
we only learn the minimum that we actually need to compete.
In each state x, we simply learn how bad it is not to be obeyed in this state.
We learn 
, which will require less memory than learning
for more than one new action.
A change of leader in the state does not give us a new quantity to learn
(i.e. we have to expand our memory dynamically).
Instead we just change the quantity of the single W-value for the state.
Another complication avoided by this strategy
is that the leading agent may be executing a confusing, non-deterministic policy
from our viewpoint, perhaps because it perceives a different state to the state that we perceive.
In this case, we could not find a single fixed action 
with which to learn .
Instead we would have to learn 
,
where action k means "do whatever agent 
would do now".
We will look more closely in §6.6
at the confusion caused by agents perceiving different subspaces.
For now we assume that all agents build up W-values for the full state x.
But note in passing that the W-value again avoids such complication
by its strategy of simply building up an averaged estimate of how bad it is not to be obeyed.
We will need more than one sample to build up a proper estimate.
W-learning (introduced in [Humphrys, 1995])
is a way of building up such an estimate when agents do not share the same suite of actions.
When agent is the winner
and has its action executed, all agents 
except update:
for 
,
but note that the reward and next state y
were caused by rather than by agent itself.
The reason why we do not update
is explained later.
When we see a difference term between predicted and actual,
we expect that this "error term" will go to zero,
but note that here it goes to a positive number.
For example, in the discrete case of W-learning, where we store each explicitly in lookup tables, we update:
where 
takes successive values 
.
Since the rewards and Q-values are bounded,
it follows that the W-values are bounded (Theorem B.3).
Using such a measure of W, an agent will not need explicit knowledge about who it is competing with. Similar to how Q-learning works, a W-learning agent need only have local knowledge - what state x we were in, what action a it suggested, whether it was obeyed or not, what state y we went to, and what reward r that gave it. It will be aware of its competition only indirectly, by the interference they cause. It will be aware of them when they stop its action being obeyed, and will be aware of the y and r caused as a result. The agent will learn W by experience - by actually experiencing what the other agents want to do.
In fact, I considered not even telling the agent whether it was obeyed, but it seems there is no satisfactory way of doing this. §6.3 shows that the obeyed agent must be treated differently from the unobeyed.
In pseudocode, the W-learning method is, every time step:
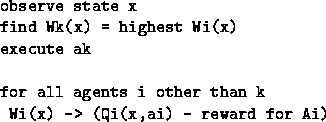
The change of W's mean that next time round in state x
there may be a different winner, and so on.
Note that by reward for Ai
we really mean the combination of immediate reward and next state.
The important thing to remember in comparing Q-learning and W-learning is that they are solving different problems. Q-learning is solving the RL problem (choosing the action in pursuit of one goal). W-learning is solving the Action Selection problem (choosing the agent in timeslicing of multiple goals).
W-learning is not another method of RL. It is not a competitor of Q-learning.
Consider Q-learning as the process:
where we are learning D, and d is caused by the execution of our action. Then W-learning is:
where D is already learnt, and f is caused by the execution of another agent's action. In the discrete case, Q-learning would be:
and W-learning would be:
this is confusing because it looks like a standard way [Sutton, 1988] of writing the Q-learning update:
where the expected value of the error term (d-D) goes to zero as we learn. But this is not the same error term as in W-learning:
In general, we assume that Q is learnt before W.
Either we delay the learning of W (see [Humphrys, 1995, §3.1])
or, alternatively, imagine a dynamically changing collection
with agents being continually created and destroyed over time,
and the surviving agents adjusting their W-values as the nature of their competition changes.
Q is only learnt once, right from the start of the life of the agent,
whereas W is relearnt again and again.
The skill that learns, expressed in its converged Q-values,
remains intact through subsequent competitions for x.
Once it learns its action 
it will promote it in all competitions,
only varying the strength with which it is promoted, as its competition varies
(this is why we only need to keep values, not 
values).
In the long term, the single-step update for is approximated by:
where and y are caused by the leader .
Note that even though keeps suggesting the same action,
we have probabilistic transitions
so and y are not constant but are random variables.
We can write this as:
where the deviation 
(the loss that causes for by being obeyed in state x)
is now not a fixed quantity as in §5.5.1
but a random variable.
The function 
is fixed, so any variation in
is caused only by the variation in and y,
which is caused by the variation in 
and 
(where 
).
We already know that is a stationary distribution.
We will assume that, even though 's action a is unrecognised by ,
we still have some stationary distribution .
If so, then will be stationary, with expected value:
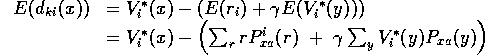
We expect:
though we do not actually update ,
and we expect for :
That is, if obeyed, we expect f = D.
If not obeyed, we expect
.[1]
We cannot calculate 
analytically
unless we know and .
So instead, as in Q-learning, we calculate it by sampling it.
If
leads forever in state x, then by Theorem A.1:
This convergence will be interrupted if some new agent takes the lead.
itself might increase so that 
and then takes the lead in state x.
If it does, W-learning stops for it until (if ever) it loses the lead.
If another agent 
takes the lead by building up a high 
,
then will suddenly be taking samples from
the distribution 
.
By Theorem A.2, if we update forever from this point,
converges to the expected value of the new distribution:
and so on.
W-learning is an approximation of the walk through the matrix that we saw in §5.6. Instead of direct assignments to the expected loss, we have to take samples of the distribution of losses.
W-learning does this walk
because we cannot exhaustively search all combinations k,i to find
the highest in the matrix (or whatever we decide would be the fairest winner).
It would be impractical to let every agent experience what it is like
with every other agent in the lead
for long enough to build up an expected value for each one.
And it would also require memory to build up a map of the matrix and return to a past leader.
W-learning tries to get down to a winner quicker than that.
We just put someone into the lead, and it's up to the others
to raise their W-values to pass it out.
Anyone who can manage a higher W-value is allowed overtake.
Just as in Q-learning - where we don't actually have to wait for an infinite time for it to be useful,
it will fixate on one or two actions fairly quickly
- so in W-learning
we don't actually require Q-learning to have converged
and we don't have to wait to get to the expected value of for there to be a switch of leader.
W-learning rapidly gets down to a competition involving only one or two agents.
The switches of leader trail off fairly quickly as W rises.
In each state x, competition will be resolved when some agent ,
as a result of the deviations it suffers in the earlier stages of W-learning,
accumulates a high enough W-value such that:
As in the walk, the reason why the competition converges
is that for the leader to keep changing,
W must keep rising.
While there may be statistical variations[2]
of in any finite sample,
in the long run the expected values must emerge,
and the walk of §5.6 will take place.
wins because it has suffered a greater deviation in the past
than any expected deviation it is now causing for the other agents.
The agent that wins is the agent that would suffer the most
if it did not win.
Think of it as perhaps many agents "wanting" the state,
but wanting it the most.
Since all 
,
we normally expect 
for it to win.
W-learning resolves competition
without resorting to devices such as killing off agents that are disobeyed for time t,
without any 
,
and in fact with normally most 
.
There will be a different competition in each state x, each being resolved at different times. Eventually, the entire statespace will have been divided up among the agents, with a winner for each state x.
So why don't we update the leader's W-value as well? The answer is that if we do, we would be updating:
The leader's W is converging to zero,
while the other agents' W's are converging to .
They are guaranteed to catch up with it.
We might think it would be nice to try and reduce all weights to the minimum possible,
so as soon as you are obeyed, you start reducing your weight.
But you can only find the minimum by reducing so far that someone else takes over.
As soon as an agent gets into the lead, its W-value would start dropping until it loses the lead.
We will have back and forth competition forever under any such system,
whereas we want someone to actually win the state.
If we do for all i including k:
then 
stays the same,
while (unless they are suffering zero) the other 
and overtake it.
If we do for all i including k:
then 
,
while (unless they are suffering zero) the other 
some quantity > 0 and overtake it.
So we can't have the same rule for the leader as for the others.
The leader does nothing - it's up to the others to catch up with it.
If they can't, we have a resolved competition.
Not scoring the leader leads to a potential problem however.
If somehow gets set to an unfairly large value,
then it will never get corrected,
since the other agents will be unable to catch up to it.
This can happen if it gets initialised randomly to some large value.
Note that 
(Theorem B.3).
Any W-value 
will eventually be challenged since we expect .
However, a W-value in the range 
may never be challenged.
The solution is that we initialise all
to be in the range 
.
They can be random within that range
since 
will wipe out the initial value in the first update.
But an unfairly high can also happen because of unlucky samples.
Say one time wasn't in the lead in state x, and it experienced:
where 
is a sample from the very high end of the distribution
with expected value 
.
normally won't suffer this when 
is in the lead,
but this single unlucky update puts into the lead
and its W-value is never challenged after that.
The other W's all converge to their expected values ,
but does not converge to anything.
It remains representing this single unlucky sample.
The solution is still not to score the leader's W-value, at least not while it is in the lead. Rather, we make sure that its W-value is updated a few times before it can take the lead forever. It can't win based on just one sample.
The solution is to pick the highest W with a Boltzmann distribution that starts at a moderately high temperature (pick a stochastic winner centred on the highest W) and declines over time. We still only score the ones that aren't obeyed. We reduce the temperature until we end up with one winner, the others converging to the deviation it causes them. As before, we aim to have the finished creature end up with just a low temperature Boltzmann rather than brittle strict-determinism.
To be precise, when we observe state x, we obey agent with probability:
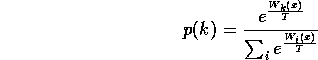
Note that 
.
The advantage of this
is that if we start with a high temperature (pick random winners),
it allows W-values to start totally random.
We don't need an initialisation strategy any more.
The analysis in §6.2 showed that if agent leads in state x, then:
But this assumes that the x in refers to the full state.
What if our agents, which are already only learning Q-values in
subspaces,
were to only build up their W-values in subspaces too?
The problem with this is that there may be many different leaders
for the many different full states which sees as all the one state.
And even if there was just one leader, what sees as one state
is seen by the leader as a number of different states
so it will be executing different actions, causing quite different deviations for .
From 's point of view, sometimes the leader executes a good action,
sometimes a bad one, for no apparent reason.
But instead of this simply being samples from different ends of a distribution,
we are actually taking samples from different distributions.
In short, we are not repeatedly updating:
for a single distribution with expected value .
Rather we are updating:
for many different distributions 
,
representing different k's and different x's.
By Theorem A.4:
where p(j) is the probability of taking a sample from
.[3]
So we coalesce the expected values of multiple distributions into one W-value.
This is a weighted mean since 
.
It is a rather crude form of competition. While Q-learning with subspaces is just as good for learning the policy as Q-learning with full space, W-learning with subspaces might not be as "intelligent" a form of competition as W-learning with full space. The agent doesn't need the full space to learn its own policy, but it may need it to talk to other agents.
We will return to this in §10.
For now, we use both Q-learning and W-learning with subspaces
for the sake of the tiny memory requirements this method will have.
's W-value is a weighted mean
of all the separate W-values that it would have
if it was able to distinguish the states.
While all these W-values have been compressed into one W-value,
it is done fairly.
The more likely it is to experience a deviation ,
the more biased will be in the direction of 
.
With W-learning with subspaces, we can add new sensors dynamically, with new agents to make use of them, and the already-existing agents will just react to it as more competition, of the strange sort where sometimes in the same state (as they see it) they are opposed and sometimes not (Figure 6.1).
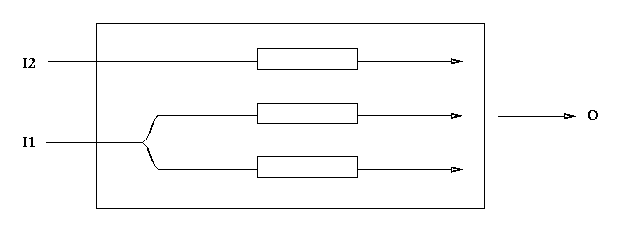
Figure 6.1: Agents may compete with each other despite sharing no common sensors.
The abstract "full" state here is 
,
though nothing in the creature works with this full state.
Recall the "map" of the statespace that we suggested drawing in §5, showing who wins each state. When agents work in subspaces only, the creature as a whole can still draw up a map of the full state-space. A W-value built up by an agent in a sub-state will typically be enough to win only some of the full states that the sub-state maps to, and lose others. The agent itself could not draw up a map of its statespace, since it could not classify its x as either "won" or "lost".
Note how concepts are becoming distributed in this model. For example, in our House Robot problem, there is now no central Perception area where the concepts of both "dirt" and "smoke" coexist. One agent solves the perception problem of distinguishing dirt from non-dirt. Another agent solves the different problem of separating smoke from non-smoke. Each solves the problem of vision to the level of sophistication necessary for its own purposes - nobody directly solves the problem of separating dirt from smoke. Agents existing in different sensory worlds are competing against each other.
Hierarchical Q-learning with subspaces looks like this too except that the switch must know about the full state-space.
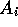has learnt the optimal action given its statespace,
action set and reward distribution,
an agent 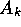that is connected to different senses or actions of the body
may suggest things that are actually better for ,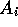
things that 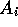is not able to learn itself because it is denied access to some senses or actions.
In such a case it would positively pay 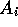not to be obeyed
(we will show such a case later).
Our model can actually cope with this - 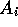will simply develop negative W-values
and not compete.
We will return to this whole issue in §18.
For the moment we will assume that agents know best what is good for themselves,
that is, that they will suffer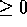 
if not obeyed.
[2]
For example, the one that takes the lead may not actually be the one with the
worst expected loss.
This is what I allowed for in [Humphrys, 1995, §4],
where the longer walk will terminate within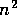 
steps.
In fact, the one that takes the lead mightn't even have
an expected loss worse than ,
it might just be an unlucky sample.
[3] Assuming this probability is stationary. What we are talking about here is, given that the agent observes a certain subspace state, what is the probability that this is really a certain full space state?
Return to Contents page.